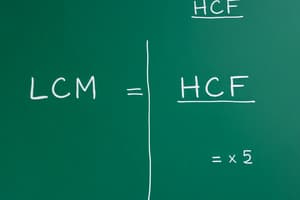Questions and Answers
What is the least common multiple (LCM) of the fractions 1/2 and 3/5?
Which statement correctly outlines the first step in finding the LCM of two fractions?
How do you determine the LCM of the algebraic expressions x^3 and x^2y?
When finding the LCM of the expressions 3x^2 and 6xy, what is the GCD you will use for the denominators?
Signup and view all the answers
What is the final step to calculate the LCM of the fractions 4/9 and 2/5?
Signup and view all the answers
In determining the LCM of the expressions 2xy and 5x^2y^3, what unique factor would you take?
Signup and view all the answers
Study Notes
LCM of Fractions
-
Definition: The least common multiple (LCM) of fractions is the smallest fraction that can be formed as a multiple of the given fractions.
-
Formula:
- LCM(a/b, c/d) = LCM(a, c) / GCD(b, d)
-
Steps to Find LCM of Fractions:
- Find the LCM of the numerators.
- Find the GCD of the denominators.
- Divide the LCM of the numerators by the GCD of the denominators.
-
Example:
- For fractions 2/3 and 3/4:
- LCM of 2 and 3 = 6
- GCD of 3 and 4 = 1
- LCM(2/3, 3/4) = 6/1 = 6
- For fractions 2/3 and 3/4:
LCM in Algebraic Expressions
-
Definition: The LCM of algebraic expressions is the smallest expression that can be divided by each of the given expressions without leaving a remainder.
-
Steps to Find LCM:
- Factor each expression into its prime factors (including variable factors).
- Identify all unique factors from the expressions.
- For each unique factor, take the highest power that appears in any of the expressions.
- Multiply these factors together to get the LCM.
-
Example:
- For expressions x^2y and xy^2:
- Factors of x^2y: x^2, y
- Factors of xy^2: x, y^2
- Highest powers: x^2 (from x^2y), y^2 (from xy^2)
- LCM = x^2y^2
- For expressions x^2y and xy^2:
-
General Note: When finding the LCM of algebraic expressions, treat each variable and its exponent similarly to how you would treat numerical factors.
LCM of Fractions
- LCM of fractions is the smallest fraction that can be formed as a multiple of the given fractions.
- The formula for LCM of two fractions ( \frac{a}{b} ) and ( \frac{c}{d} ) is:
LCM(a/b, c/d) = LCM(a, c) / GCD(b, d) - Steps to calculate the LCM of fractions:
- Calculate the LCM of the numerators.
- Determine the GCD of the denominators.
- Divide the LCM of the numerators by the GCD of the denominators.
- Example using 2/3 and 3/4 demonstrates:
- LCM(2,3) is 6.
- GCD(3,4) is 1.
- Thus, LCM(2/3, 3/4) equals 6.
LCM in Algebraic Expressions
- LCM of algebraic expressions is the smallest expression that can be divided by each expression without a remainder.
- Steps to find LCM of algebraic expressions include:
- Factor each expression into prime factors, including variable factors.
- Identify all unique factors present in the expressions.
- For each unique factor, take the highest power appearing in any expression.
- Multiply the factors to derive the LCM.
- Example using ( x^2y ) and ( xy^2 ):
- Factors of ( x^2y ) are ( x^2 ) and ( y ).
- Factors of ( xy^2 ) are ( x ) and ( y^2 ).
- The highest powers identified: ( x^2 ) (from ( x^2y )) and ( y^2 ) (from ( xy^2 )).
- Therefore, LCM = ( x^2y^2 ).
- Important note: Treat variables and their exponents during LCM calculation similarly to numerical factors.
Studying That Suits You
Use AI to generate personalized quizzes and flashcards to suit your learning preferences.
Description
Explore the concepts of least common multiple (LCM) as applied to fractions and algebraic expressions. This quiz will test your understanding of the definitions, formulas, and steps involved in finding the LCM in both numeric and algebraic contexts. Get ready to solve problems and enhance your math skills!
