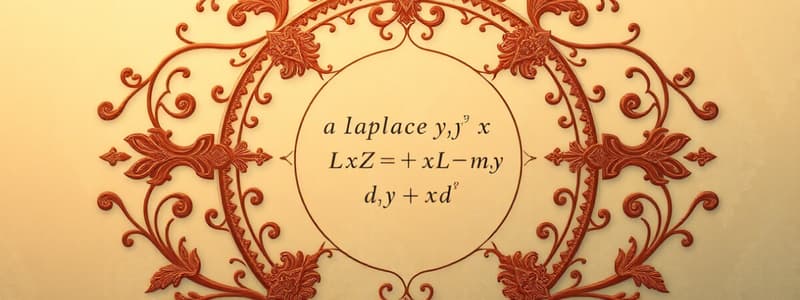Podcast
Questions and Answers
Which method is most suitable for solving the given Laplace equation with a source term and zero boundary conditions on a square?
Which method is most suitable for solving the given Laplace equation with a source term and zero boundary conditions on a square?
- Direct integration
- Finite element method
- Using Green's functions
- Separation of variables with Fourier series expansion (correct)
Given the equation $-4u + 3u_{xx} + u_{yy} + sin(2x) = 0$ and assuming a solution of the form $u(x, y) = \sum_{m=1}^{\infty} \sum_{n=1}^{\infty} A_{mn}sin(mx)sin(ny)$, what equation must $A_{mn}$ satisfy?
Given the equation $-4u + 3u_{xx} + u_{yy} + sin(2x) = 0$ and assuming a solution of the form $u(x, y) = \sum_{m=1}^{\infty} \sum_{n=1}^{\infty} A_{mn}sin(mx)sin(ny)$, what equation must $A_{mn}$ satisfy?
- $(-4 - 3m^2 - n^2)A_{mn} + \int_{0}^{\pi} \int_{0}^{\pi} sin(2x) dxdy = 0$
- $(-4 + 3m^2 + n^2)A_{mn} = 0$
- $(-4 - 3m^2 - n^2)A_{mn} + \int_{0}^{\pi} \int_{0}^{\pi} sin(2x)sin(mx)sin(ny) dxdy = 0$ (correct)
- $(-4 - 3m^2 - n^2)A_{mn} = 0$
In solving $-4u + 3u_{xx} + u_{yy} + sin(2x) = 0$ with $u(x, y) = \sum_{m=1}^{\infty} \sum_{n=1}^{\infty} A_{mn}sin(mx)sin(ny)$, for what values of $m$ and $n$ will $\int_{0}^{\pi} sin(2x)sin(mx) dx$ be non-zero?
In solving $-4u + 3u_{xx} + u_{yy} + sin(2x) = 0$ with $u(x, y) = \sum_{m=1}^{\infty} \sum_{n=1}^{\infty} A_{mn}sin(mx)sin(ny)$, for what values of $m$ and $n$ will $\int_{0}^{\pi} sin(2x)sin(mx) dx$ be non-zero?
- For all integer values of $m$
- Only when $n = 0$
- Only when $m = 0$
- Only when $m = 2$ (correct)
Given the equation $-4u + 3u_{xx} + u_{yy} + sin(2x) = 0$ with zero boundary conditions, and the solution form $u(x, y) = \sum_{m=1}^{\infty} \sum_{n=1}^{\infty} A_{mn}sin(mx)sin(ny)$, which expression correctly describes $A_{2n}$?
Given the equation $-4u + 3u_{xx} + u_{yy} + sin(2x) = 0$ with zero boundary conditions, and the solution form $u(x, y) = \sum_{m=1}^{\infty} \sum_{n=1}^{\infty} A_{mn}sin(mx)sin(ny)$, which expression correctly describes $A_{2n}$?
If the solution to $-4u + 3u_{xx} + u_{yy} + sin(2x) = 0$ is given by $u(x, y) = \sum_{n=1}^{\infty} A_{2n}sin(2x)sin(ny)$ and $A_{2n} = \frac{c}{(-16 - n^2)}$, what happens to the amplitude of higher modes as n increases?
If the solution to $-4u + 3u_{xx} + u_{yy} + sin(2x) = 0$ is given by $u(x, y) = \sum_{n=1}^{\infty} A_{2n}sin(2x)sin(ny)$ and $A_{2n} = \frac{c}{(-16 - n^2)}$, what happens to the amplitude of higher modes as n increases?
Flashcards
Laplace Equation
Laplace Equation
A second-order partial differential equation that describes the steady-state distribution of a potential, such as temperature or voltage.
Solution to Laplace Equation
Solution to Laplace Equation
A function, u(x,y), whose Laplacian (sum of second-order partial derivatives) equals zero.
Boundary Conditions
Boundary Conditions
Conditions specifying the value of the unknown function on the boundary of the domain.
Given Problem
Given Problem
Signup and view all the flashcards
Particular Solution
Particular Solution
Signup and view all the flashcards
Study Notes
- The task is to solve the Laplace equation: -4u + 3u_xx + u_yy + sin(2x) = 0
- The equation needs to be solved on a square where 0 < x, y < π.
- The boundary conditions are zero, meaning u = 0 on the top, bottom, left, and right sides of the square.
Studying That Suits You
Use AI to generate personalized quizzes and flashcards to suit your learning preferences.