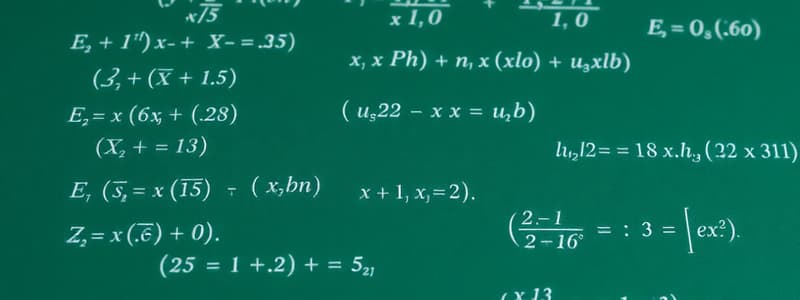Podcast
Questions and Answers
Given that the equation $2x^2 + (a - 5)x + 15 = 3a$ has no real roots, and the solution set for a is the interval $(\alpha, \beta)$, what is the sum of the squares of all integers within this interval, represented as $\sum x^2$?
Given that the equation $2x^2 + (a - 5)x + 15 = 3a$ has no real roots, and the solution set for a is the interval $(\alpha, \beta)$, what is the sum of the squares of all integers within this interval, represented as $\sum x^2$?
- 2119
- 2109
- 2129
- 2139 (correct)
If $\sin(x) + \sin^2(x) = 1$ where $x \in [0, \frac{\pi}{2}]$, what is the value of the expression $(\cos^{12}(x) + \tan^4(x)) + 3(\cos^{10}(x) + \tan^{10}(x)) + (\cos^6(x) + \tan^6(x))$?
If $\sin(x) + \sin^2(x) = 1$ where $x \in [0, \frac{\pi}{2}]$, what is the value of the expression $(\cos^{12}(x) + \tan^4(x)) + 3(\cos^{10}(x) + \tan^{10}(x)) + (\cos^6(x) + \tan^6(x))$?
- 2 (correct)
- 3
- 1
- 4
The area enclosed by the curves $|y| = 1 - x^2$ and $x^2 + y^2 = 1$ is given by $\alpha$. If $9\alpha = \beta\pi + \gamma$, where $\beta$ and $\gamma$ are integers, what is the value of $|\beta - \gamma|$?
The area enclosed by the curves $|y| = 1 - x^2$ and $x^2 + y^2 = 1$ is given by $\alpha$. If $9\alpha = \beta\pi + \gamma$, where $\beta$ and $\gamma$ are integers, what is the value of $|\beta - \gamma|$?
- 33 (correct)
- 27
- 15
- 18
The domain of the function $log_8(18x - x^2 - 77)$ is $(\alpha, \beta)$, and the domain of the function $log_{(x-1)}\left(\frac{2x^2 + 3x - 2}{x^2 - 3x - 4}\right)$ is $(\gamma, \delta)$. What is the value of $\alpha^2 + \beta^2 + \gamma^2$?
The domain of the function $log_8(18x - x^2 - 77)$ is $(\alpha, \beta)$, and the domain of the function $log_{(x-1)}\left(\frac{2x^2 + 3x - 2}{x^2 - 3x - 4}\right)$ is $(\gamma, \delta)$. What is the value of $\alpha^2 + \beta^2 + \gamma^2$?
Given $f(x) = (x^2 - 1)|x^2 - ax + 2| + \cos(|x|)$, and that $f(x)$ is non-differentiable at exactly two points, $x = \alpha$ and $x = \beta$, find the distance of the point $(\alpha, \beta)$ from the line $12x + 5y + 10 = 0$.
Given $f(x) = (x^2 - 1)|x^2 - ax + 2| + \cos(|x|)$, and that $f(x)$ is non-differentiable at exactly two points, $x = \alpha$ and $x = \beta$, find the distance of the point $(\alpha, \beta)$ from the line $12x + 5y + 10 = 0$.
A straight line L passes through the point P(2, -1, 3) and is perpendicular to the lines $\frac{x+1}{2} = \frac{y-2}{-2} = \frac{z+3}{1}$ and $\frac{x-1}{1} = \frac{y+1}{3} = \frac{z}{4}$. If L intersects the yz-plane at point Q, what is the distance between P and Q?
A straight line L passes through the point P(2, -1, 3) and is perpendicular to the lines $\frac{x+1}{2} = \frac{y-2}{-2} = \frac{z+3}{1}$ and $\frac{x-1}{1} = \frac{y+1}{3} = \frac{z}{4}$. If L intersects the yz-plane at point Q, what is the distance between P and Q?
Let $S = \mathbb{N} \cup {0}$. A relation R is defined from S to $\mathbb{R}$ as $R = {(x, y): \log_e y = x \log_2(\frac{2}{3}), x \in S, y \in \mathbb{R}}$. What is the sum of all the elements in the range of R?
Let $S = \mathbb{N} \cup {0}$. A relation R is defined from S to $\mathbb{R}$ as $R = {(x, y): \log_e y = x \log_2(\frac{2}{3}), x \in S, y \in \mathbb{R}}$. What is the sum of all the elements in the range of R?
The line $x + y = 1$ intersects the x and y axes at points A and B, respectively. A right-angled triangle AMN is inscribed within triangle OAB (where O is the origin), with M and N lying on OB and AB, respectively. If the area of triangle AMN is $\frac{4}{9}$ that of triangle OAB, and $\frac{AN}{NB} = \frac{\lambda}{1}$, then what is the sum of all possible value(s) of$\lambda$?
The line $x + y = 1$ intersects the x and y axes at points A and B, respectively. A right-angled triangle AMN is inscribed within triangle OAB (where O is the origin), with M and N lying on OB and AB, respectively. If the area of triangle AMN is $\frac{4}{9}$ that of triangle OAB, and $\frac{AN}{NB} = \frac{\lambda}{1}$, then what is the sum of all possible value(s) of$\lambda$?
If $40x + 18y = 109$ is the equation of the chord of the ellipse $\frac{x^2}{9} + \frac{y^2}{4} = 1$ whose midpoint is $(\frac{5}{2}, \frac{1}{2})$, what is the value of $\alpha + \beta$?
If $40x + 18y = 109$ is the equation of the chord of the ellipse $\frac{x^2}{9} + \frac{y^2}{4} = 1$ whose midpoint is $(\frac{5}{2}, \frac{1}{2})$, what is the value of $\alpha + \beta$?
If all possible words, with or without meaning, that can be formed using the letters of 'KANPUR' are arranged as in a dictionary, at what position is the word 'PRKAUN'?
If all possible words, with or without meaning, that can be formed using the letters of 'KANPUR' are arranged as in a dictionary, at what position is the word 'PRKAUN'?
Let $A = [a_{ij}]$ be a 3x3 matrix where $a_{ij} = (\sqrt{2})^{i+j}$. If the sum of all the elements in the third row of $A^2$ is $\alpha + \beta\sqrt{2}$, where $\alpha, \beta \in \mathbb{Z}$, what is the value of $\alpha + \beta$?
Let $A = [a_{ij}]$ be a 3x3 matrix where $a_{ij} = (\sqrt{2})^{i+j}$. If the sum of all the elements in the third row of $A^2$ is $\alpha + \beta\sqrt{2}$, where $\alpha, \beta \in \mathbb{Z}$, what is the value of $\alpha + \beta$?
Let $\alpha, \beta$ ($\alpha \ne \beta$) be the values of m for which the given system of equations has infinitely many solutions. What is the value of $\sum_{n=1}^{10} (n^\alpha + n^\beta)$?
Let $\alpha, \beta$ ($\alpha \ne \beta$) be the values of m for which the given system of equations has infinitely many solutions. What is the value of $\sum_{n=1}^{10} (n^\alpha + n^\beta)$?
Point P(1, 2, 2) has a perpendicular line to L; the line meets L at Q; what is 2PQsquared?
Point P(1, 2, 2) has a perpendicular line to L; the line meets L at Q; what is 2PQsquared?
A circle runs through 4,2 and 0,2 and has its centre by the line 3x+2y+2. What length of chord lies mid point is 1,2?
A circle runs through 4,2 and 0,2 and has its centre by the line 3x+2y+2. What length of chord lies mid point is 1,2?
A 2*2 matrix equals alj0,1. X gives what of a matrix A variance is
A 2*2 matrix equals alj0,1. X gives what of a matrix A variance is
Alpha is: limit of x approaching 0
Alpha is: limit of x approaching 0
If y is dependent on something tanx and other stuff is satisfied and with stuff: stuff
If y is dependent on something tanx and other stuff is satisfied and with stuff: stuff
For this expression select correct answers.
For this expression select correct answers.
If (3x2+5)dx 8/(5e5), then selection of alpha is.
If (3x2+5)dx 8/(5e5), then selection of alpha is.
Select the value so expression a=a2024.
Select the value so expression a=a2024.
Find total all possible ordered pairs if zeC is related for the conditions:
Find total all possible ordered pairs if zeC is related for the conditions:
What does it equals to if focal is what.
What does it equals to if focal is what.
Flashcards
What is the interval (α, β)?
What is the interval (α, β)?
Set of all 'a' ∈ R, for which 2x² + (a-5)x + 15 = 3a has no real root
Value of (cos²x + tan¹²x) + 3(cos¹°x +tan¹°x + cos⁶x + tan⁶x) + (cos⁴x + tan⁴x)
Value of (cos²x + tan¹²x) + 3(cos¹°x +tan¹°x + cos⁶x + tan⁶x) + (cos⁴x + tan⁴x)
If sinx + sin²x = 1, the given expression equals 2
What is |β - γ| given area α enclosed by |y| = 1 - x² and x² + y² = 1?
What is |β - γ| given area α enclosed by |y| = 1 - x² and x² + y² = 1?
If 9α = βπ + γ, the absolute difference between β, γ is 33.
Value of α² + β² + γ²?
Value of α² + β² + γ²?
If the domain of log₈(18x - x² - 77) is (α, β) and the domain of log(x-1) ((2x²+3x-2) / (x²-3x-4)) is (γ, δ), then α² + β² + γ² is 186
Signup and view all the flashcards
Distance between points P and where L intersects yz-plane?
Distance between points P and where L intersects yz-plane?
Let a straight line L pass through P(2,-1,3) and be perpendicular to given lines. The distance is 3
Signup and view all the flashcards
Sum of all elements in Range of R?
Sum of all elements in Range of R?
R is a relation from S to R and the sum of range elements is 10/3
Signup and view all the flashcards
If AN:NB = λ : 1, sum of all possible values of λ?
If AN:NB = λ : 1, sum of all possible values of λ?
Line meets axes at A,B. A right triangle AMN is inscribed and the sum of all the possible values is 13/6
Signup and view all the flashcards
If aX + bY = 109 is equation of chord of ellipse + = 1 & midpoint (5/2,1/2)
If aX + bY = 109 is equation of chord of ellipse + = 1 & midpoint (5/2,1/2)
If 40x + 18y = 109 the sum α+β=58
Signup and view all the flashcards
Word at 440th position after dictionary arrangement?
Word at 440th position after dictionary arrangement?
Words with/without meaning using 'KANPUR', at 440th position the arrangement is PRKAUN
Signup and view all the flashcards
If A=[√2^(i+j)], find α + β
If A=[√2^(i+j)], find α + β
Third-row elements sum is α + β√2 and then α + β equals 224
Signup and view all the flashcards
Value of Σ (n³+n)
Value of Σ (n³+n)
If infinitely many solutions then value of sigma is 440
Signup and view all the flashcards
The Value of 2(PQ)²
The Value of 2(PQ)²
The line L: intersects the line L at Q and 2(PQ)² =27
Signup and view all the flashcards
What is the Length mid-point circle is (1,2)
What is the Length mid-point circle is (1,2)
If the length of the chord, of the circle C, whose mid-point is (1, 2) then the length is 2√3
Signup and view all the flashcards
Best suited Answer in all the 4 statements
Best suited Answer in all the 4 statements
Magnetic flux is the term which provides the answer (A)-(II), (B)-(I), (C)-(IV), (D)-(III)
Signup and view all the flashcards
Give the type for each term of (A), (B), (C), (D) of all applications
Give the type for each term of (A), (B), (C), (D) of all applications
Transistor is the the application among all the statements
Signup and view all the flashcardsStudy Notes
- These are study notes from a JEE-Main Examination in January 2025
Mathematics:
Section A:
-
If the equation 2x² + (a-5)x + 15 = 3a has no real root for all a ∈ R, then a is in the interval (-19, 5); Therefore sum of the squares of integers between -19 and 5 i.e ∑x² = 2139
-
If sinx + sin²x = 1, then (cos¹²x + tan¹²x) + 3(cos¹°x + tan¹°x + cosx + tanx) + (cos⁸x + tan⁸x) is equal to 2. sinx = cos²x ⇒ tanx = cosx
-
The area enclosed by |y| = 1 − x² and x² + y² = 1 is α = (π − 8/3); if 9α = βπ + γ; then |β − γ| = 33. β = 9, γ = −24
-
The domain of log(18x−x²−77) is (7, 11), and the domain of log(x−1)(2x²+3x−2)/(x²−3x−4) is (4, ∞); Therefore if the domains are (α, β) and (γ, δ) respectively, then a² + β² + γ² = 186
-
f(x) = (x²−1)|x²−ax+2| + cos|x| is not differentiable at x = −2 and x = β; the distance of the point (α, β) from the line 12x + 5y + 10 = 0 is equal to 3. cosx is always differentiable, check only for |x² − ax + 2
-
A straight line L passes through P(2,−1,3) and is perpendicular to (x−3)/1 = (y+1)/(−1) = (z−2)/2 and (x)/(3) = (y−4)/(4) = (z+2)/(−2). If L intersects the yz-plane at point Q, then the distance between P and Q is 3. Vector parallel to 'L' = 5(2î − 2j + k). Equation of 'L': (x−2)/(2) = (y+1)/(−2) = (z−3)/(1) = λ (say)
-
Set S = N ∪ {0}; Define a relation R from S to R by: R = {(x, y) : loge y = xloge(2/5) }; Then, the sum of all the elements in the range of R is 10/9
-
The line x + y = 1 meets the x and y axes at A and B. A right-angled triangle AMN is inscribed in triangle OAB, where O is the origin, and M and N lie on OB and AB. Area of triangle AMN is 4/9 of the area of triangle OAB, and AN : NB = λ : 1; therefore the sum of all possible values of λ = 13/6
-
If 40x + By = 109 is the equation of the chord of the ellipse (x²/9) + (y²/4) = 1 whose midpoint is (5/2, 1/2) then α + β = 58
-
If all words with or without meaning are made using the letters of the word "KANPUR" and arranged as in a dictionary, the word at the 440th position is PRKAUN
-
Let A = [aij] be a 3 × 3 matrix with aij = (√2)^(i + j)⁻¹. If the sum of all the elements in the third row of A² is α + β√2, then α + β = 224
-
Let P be the foot of the perpendicular from (1, 2, 2) on the line L: (x−1)/(−1) = (y+1)/(1) = (z−2)/(2) ; the line intersects Lat Q, then 2(PQ)² = 27
-
If cos(π/3) = â • (i + αj + k) / (√|1 + α² + 1|), then α = −√6. â is a unit vector perpendicular to b = î − 2j + 3k and c = 2î + 3j − k, and makes an angle of cos⁻¹(2/3) with the vector î + j + k
-
If y • sec x = ∫(2 + sec x)/(1 + 2sec x)² dx, then f(π/4) = (4 − √2)/14. dy/dx + (tan x)y = (2 + sec x) /(1 + 2sec x)²
-
If ∫₀^(π/12) |24(sin 4x + [2sin x])| dx = 2 + α, where [•] represents the greatest integer function, then α = 12
-
If lim(t→0) [∫₀^(t) (3x + 5)^(8/3) dx] / [(5e)^(α/5)] = (64/5), then α = 64
-
Given z ≠ 1, z ∈ C, where and are the roots of x² + x + 1 = 0, |(z −ω) / (z+ω²) + (z+ω) / (z⁻ω²| = 1, if a+b≠0 for integers a, b ∈ [−3,3] then the number of pairings = 10
-
The sum of terms in equidistant from beginning = S203 = 2233 for a1, a2, ..., a2024 be an Arithmetic Progression and a1 + (a5 + a10 + a15 + ... + a2020) + a2024 = 2233. The sum equals 11132.
-
If for integers a, b is in [-3, 3]a + b ≠ 0 then the number of all pairings = 10
-
For a given vertex 3 equal masses interact at equilibrium = 3/2
Section B:
- When a sand dropper drops sand of mass m(t) on a conveyer belt at a rate proportional to the square root of speed (v), the power is delivered to run the belt (P²) α v⁵
Physics:
Section A:
-
To harvest heat energy from temperature differences, the material should have low thermal conductivity and high electrical conductivity.
-
Assertion (A): In an isothermal process, PV = constant. Reason (R): During adiabatic process the volume falls off more rapidly. Both are true.
-
Torque on dipole is zero and potential energy is minimum.
-
Stopping potential is hC/λ = W + eVS
-
A poly-atomic molecule (Cᵥ = 3R, Cₚ = 4R goes from space point with isothermal path. A=10⁴ pascal, Va=(410^-6) B( PA=510⁴ ), Vb=(6*10^-6) C= (p=10⁴). The net rate of heat absorbed per limit mole is 450R((im 4+im3)).
-
After calculating we realize two identical symmetric double convex lens with focals cut into equal length are equal
Electricity:
- To achieve equilibrium , Q1 =10 mc
- the net momentum. if equal masses interact . The net atomic momentum at the interaction point.
Chemistry:
Section A:
-
Calculated spin only magnetic moments of is a function of the hallides
-
Hydrogen like spectres: Energy is (n+n)=1390
Organic structure:
- partition graphy
Chemistry 54:
- Valine Lysine and.
Chemical reaction:
- The most stab carbocation from. Stability depends on ability of a carbon to carry a higher charge
Chemical 56:
- For concentration applied it remains same
Chemical reaction:
- For electrolysis . Statement 1: is false ; statement 2: is true
Homotropic Compounds:
- The number of electron counts,
- First initial electron counts.
Studying That Suits You
Use AI to generate personalized quizzes and flashcards to suit your learning preferences.