Geometry: Volume of Pyramid and Prism

Choose a study mode

Play Quiz
Study Flashcards
Spaced Repetition
Chat to Lesson

Podcast

Play an AI-generated podcast conversation about this lesson

Questions and Answers

What is the main concept that explains the volume of a pyramid being one-third of the volume of a prism?

  • The base area of the prism is always larger than the pyramid.
  • The apex of the pyramid is higher than the prism's height.
  • A prism can be sliced into three identical pyramids. (correct)
  • A prism can be divided into two identical prisms.

When deriving the formula for the volume of a pyramid, what role does the height play?

  • It decreases the overall volume of the pyramid.
  • It increases the base area.
  • It is the distance from the apex to the base. (correct)
  • It changes the shape of the base.

Which part of the derivation process illustrates why the volume of a pyramid is one-third that of a prism?

  • The prism contains only one pyramidal section.
  • The height of the pyramid is less than the prism.
  • The prism can be split into three identical pyramids. (correct)
  • There is an infinite number of bases in a prism.

Which statement correctly identifies the dimensions required for calculating the volume of a pyramid?

<p>Base area and height. (A)</p> Signup and view all the answers

In the context of the volume relationship between a pyramid and a prism, which of the following is a true statement?

<p>The volume of the prism is three times that of the pyramid. (D)</p> Signup and view all the answers

Which geometric principle is essential for understanding the volume relationship between a pyramid and a prism?

<p>The concept of partitioning space. (A)</p> Signup and view all the answers

What would happen to the volume calculation of a pyramid if the base area remains constant but the height is doubled?

<p>The volume would double. (A)</p> Signup and view all the answers

What is the volume of a pyramid in relation to a prism with the same base area and height?

<p>One-third the volume of the prism (A)</p> Signup and view all the answers

How is the volume of a pyramid derived using a comparison with a prism?

<p>By filling the pyramid and finding the number of equal pourings to fill the prism (B)</p> Signup and view all the answers

What is the formula for calculating the volume of a pyramid?

<p>V = (1/3) * B * h (D)</p> Signup and view all the answers

What geometric feature must be common in both a pyramid and a prism for their volume comparison?

<p>The base area of both shapes (A)</p> Signup and view all the answers

What measurement is essential for finding the volume of both pyramids and prisms?

<p>The height perpendicular to the base (A)</p> Signup and view all the answers

During the comparison between a pyramid and prism for volume determination, what is the significance of the ratio of volumes?

<p>It shows how many pyramids can fill one prism (B)</p> Signup and view all the answers

In the derivation process, after filling the pyramid with water, what must be done next?

<p>Pour the water into a prism of equal base area and height (C)</p> Signup and view all the answers

What error is commonly made when calculating the volume of a pyramid?

<p>Applying the prism's volume formula to the pyramid (A)</p> Signup and view all the answers

Flashcards

Pyramid Volume Formula

Volume = (1/3) * base area * height

Pyramid

3D shape with a polygonal base and triangular faces meeting at a point

Prism Volume Formula

Volume = base area * height

Prism

3D Shape with two parallel congruent bases and rectangular faces connecting them

Signup and view all the flashcards

Base Area (pyramid/prism)

Area of the polygon at the bottom (or top) of a pyramid/prism

Signup and view all the flashcards

Pyramid/Prism Height

Perpendicular distance between apex (pyramid) or bases (prism)

Signup and view all the flashcards

Pyramid-Prism Volume Ratio

Pyramid volume is 1/3 of a prism with the same base area & height

Signup and view all the flashcards

Volume Units

Cubic units (e.g., cm³)

Signup and view all the flashcards

Pyramid Volume Formula

Volume = (1/3) * base area * height

Signup and view all the flashcards

Prism Volume

Volume = base area * height

Signup and view all the flashcards

Pyramid Shape

3D shape with a polygonal base & triangular faces meeting at a point

Signup and view all the flashcards

Prism Shape

3D shape with 2 parallel congruent bases & rectangular faces

Signup and view all the flashcards

Base Area (3D)

Area of the polygon at the bottom (or top)

Signup and view all the flashcards

3D Height

Perpendicular distance from apex (pyramid) or bases (prism)

Signup and view all the flashcards

Pyramid-Prism Ratio

Pyramid's volume is 1/3 the prism's with the same base and height

Signup and view all the flashcards

Volume Units

Cubic units (e.g., cm³)

Signup and view all the flashcards

Study Notes

Volume of a Pyramid

  • A pyramid is a three-dimensional shape with a polygonal base and triangular faces that meet at a common vertex (apex).
  • The volume of a pyramid is calculated using the formula: Volume = (1/3) * base area * height.
    • Where:
      • Base area is the area of the polygon forming the base of the pyramid.
      • Height is the perpendicular distance from the apex to the base.
  • The formula demonstrates that the volume of a pyramid is one-third the volume of a prism with the same base and height.

Volume of a Prism

  • A prism is a three-dimensional shape with two parallel and congruent polygonal bases connected by rectangular faces.
  • The volume of a prism is calculated using the formula: Volume = base area * height.
    • Where:
      • Base area is the area of the polygon forming the base of the prism.
      • Height is the perpendicular distance between the two parallel bases.

Derivation of Pyramid Volume Formula (Conceptual)

  • To understand the formula for a pyramid's volume, consider a prism with the same base area and height as the pyramid.
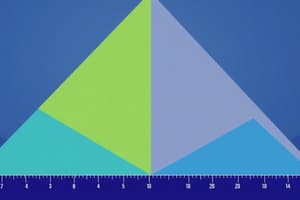
  • Imagine slicing the prism into three identical pyramids.
  • Each pyramid will have the same base as the prism and the same height as the prism.
  • Because there are three equal pyramids within the prism, the volume of one pyramid is one-third of the prism's volume.

Relationship between Pyramid and Prism Volumes

  • The relationship between the volume of a pyramid and the volume of a prism with the same base area and height is crucial.
  • This relationship is visually demonstrated by the partitioning of the prism into three equal pyramids.
  • This is a fundamental geometrical principle relating the volumes of these shapes.

Practical Application Examples

  • Calculating the volume of a square pyramid with a base side of 5 cm and a height of 10 cm.
    • First, calculate the base area (5 cm * 5 cm = 25 sq cm).
    • Then, apply the formula: (1/3)(25 sq cm)(10 cm) = 83.33 cubic cm.
  • Calculating the volume of a triangular prism with a triangular base of 4 cm x 3 cm and height of 6 cm.
    • First, calculate the area of the triangular base (0.5 * 4 cm * 3 cm = 6 sq cm).
    • Then, apply the formula: (6 sq cm)*(6 cm) = 36 cubic cm.

Studying That Suits You

Use AI to generate personalized quizzes and flashcards to suit your learning preferences.

Quiz Team

More Like This

Use Quizgecko on...
Browser
Open
Browser
Browser