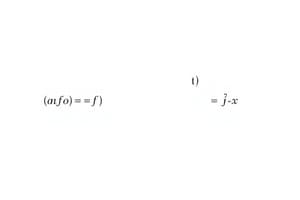Functions and Relations Lesson 1

Questions and Answers

What is the definition of a function?

A relation where each domain element corresponds to multiple range elements.

A relation that includes repeated elements in the domain.

A set of ordered pairs with no restrictions on correspondence.

A relation where each element of the domain corresponds to exactly one element of the range. (correct)

Which of the following statements about the domain and range is true?

The domain can contain repeated elements while the range cannot.

The domain is always larger than the range.

The domain is the set of first coordinates and the range is the set of second coordinates. (correct)

The range contains all x-coordinates of the ordered pairs.

What is the purpose of the vertical line test?

To compare different domain sets of functions.

To determine if a function has multiple outputs for one input.

To test if a graph of a relation is a function. (correct)

To check if the domain contains repeated values.

In a piecewise function, what does it mean when a subfunction applies to a certain portion of the main function's domain?

<p>Different expressions are used for different parts of the domain.</p> Signup and view all the answers

What happens when you perform operations on functions with overlapping domains?

<p>The operations can result in new functions that may have different domains.</p> Signup and view all the answers

Study Notes

Functions and Relations

Definitions
- Domain: Set of first coordinates in ordered pairs.
- Range: Set of second coordinates in ordered pairs.
- Examples: For pairs (1,2), (3,4), (5,6), (7,8), Domain: {1,3,5,7}, Range: {2,4,6,8}.
Relations
- Defined as a set of ordered pairs; includes a Domain and its Range.
- Domain refers to the set of all x-components, while the Range includes all y-components.
Functions
- A function relates each element of the domain to exactly one element in the range.
- Example Domain: {5,10,15,20}, Range: {2,3,4,5}.
- Values arranged in ascending order.

Representation of Functions

Functions can be represented in various forms:
- Ordered Pairs: Example: (x, y).
- Table of Values: Lists corresponding values of x and y.
- Mapping Diagram: Visual representation linking domain to range.
- Vertical Line Test: A graphical method to determine if a relation is a function; if a vertical line intersects the graph more than once, it's not a function.
Note:
- Domain values cannot be repeated while range values may repeat.

Evaluation of Functions

To evaluate a function, replace the variable x with a given value.
- Example: For h(x) = (6x - 3)/7, and find h(4):
  - h(4) = (6*4 - 3)/7 = (24 - 3)/7 = 21/7 = 3.

Piecewise Functions

Defined by multiple sub-functions, each applies to a specific domain portion.
- Example: f(x) = {4 + x for x² - 2}.
- Calculation:
  - For f(0): f(0) = 0² + 5 = 5.
  - For f(5): f(5) = 5 - 2 = 3.

Operations on Functions

Functions with overlapping domains can be:
- Added: (f + g)(x) = f(x) + g(x).
- Subtracted: (f - g)(x) = f(x) - g(x).
- Multiplied: (fg)(x) = f(x) * g(x).
- Divided: (f/g)(x) = f(x) / g(x), where g(x) ≠ 0.
These operations apply to any functions f(x) and g(x) over their common domain.

Description

Explore the fundamental concepts of functions and relations in this quiz. Understand the definitions of domain and range, and how to identify ordered pairs, domain sets, and range sets. Test your knowledge through examples and different representations such as tables and mappings.