Exploring the Multiplication Table Up to 20 x 10

Study Notes

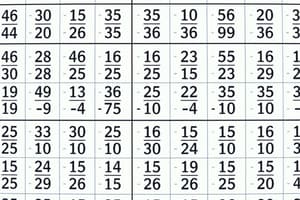
Exploring the Multiplication Table Up to 20 x 10

The multiplication table is a foundational tool that helps us understand, memorize, and perform calculations using the rules of multiplication. In this discussion, we'll dive into the specifics of the multiplication table extending from one through twenty times ten (up to (20 \times 10)).

Memorizing the Multiples

Each row within our multiplication table represents the corresponding multiple of the top number. For instance:

[ \begin{array}{|c|cccccc|} \cline{2-7} & 1 & 2 & 3 & 4 & ... & 10 \ \hline 1 & 1 & 2 & 3 & 4 & ... & 10 \ 2 & 2 & 4 & 6 & 8 & ... & 20 \ 3 & 3 & 6 & 9 & 12 & ... & 30 \ ... & ... & ... & ... & ... & ... & ... \ 10 & 10 & 20 & 30 & 40 & ... & 100 \ \end{array} ]

Knowing how to find these values will help you avoid having to memorize each entry individually.

Deriving Values Using Rules of Multiplication

If you don't yet have the whole table committed to memory, here's how to calculate any given value in the table:

Multiply the number on the left by the number above it.
- For example, to get the first element in the second column ((2 \times 2 = 4)), multiply 2 by itself.
Look for patterns in the results, which can make calculating larger numbers easier:
- If the product ends with zeroes, remove them and double the remaining digits. This pattern holds true until tens place gets involved.
  - From the table: (3 \times 7 = 21,) removing zeros leaves 2, doubling gives 4; therefore, (3 \times 8 = 24.)
Apply related addition facts like commutativity and associativity when needed:
- Commutativity allows swapping the order of factors without changing their product.
  - For example, if you want to find (7 \times 8,) recall that (7 \times 8 = 8 \times 7;) so, just look for (8 \times 7) in your mental or physical table.
- Associativity means that the grouping of operands does not affect their result.
  - Let’s say you need to find (12 \times 35.) Break down the large factor into smaller ones, applying the distributive property twice. [ 12 \times 35 = 12 \times (30 + 5) = (12 \times 30) + (12 \times 5) = 360 + 60 = 420 ]

Practical Usage Scenarios

After learning this material, its utility becomes apparent across various disciplines, including everyday math, budgeting, cooking, and science fields such as physics and chemistry.

In summary, familiarity with the multiplication table up to (20 \times 10) opens doors to numerous mathematical concepts and practical applications. Knowledge acquired through understanding rules of multiplication, discovering hidden patterns among products, and utilizing straightforward calculation techniques offers significant benefits in daily life, education, and career paths alike.

Description

Dive into the specifics of the multiplication table extending from one through twenty times ten (up to 20 x 10). Learn how to derive values, memorize multiples, and apply rules of multiplication efficiently for practical usage in various disciplines.