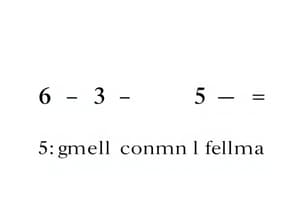Podcast
Play an AI-generated podcast conversation about this lesson
Questions and Answers
According to Euclid’s Lemma, if a prime $p$ divides $ab$, then
According to Euclid’s Lemma, if a prime $p$ divides $ab$, then
- $p$ divides $a$ and $b$
- both $a$ and $b$ are prime numbers
- $p$ does not divide $a$ and $p$ does not divide $b$
- $p$ divides $a$ or $p$ divides $b$ (correct)
What does the Fundamental Theorem of Arithmetic state?
What does the Fundamental Theorem of Arithmetic state?
- Every integer greater than 1 is a prime or a product of primes, and this product is not unique.
- Every integer greater than 1 is a prime or a product of primes, and this product is unique. (correct)
- Every integer is a prime number.
- Every integer is a composite number.
What is an example where Euclid’s Lemma may fail?
What is an example where Euclid’s Lemma may fail?
- $6$ divides $4$ and $3$
- $6$ is not a prime number
- $6$ does not divide $(4 \times 3)$
- $6$ divides $(4 \times 3)$ but does not divide $4$ or $3$ (correct)
What does Euclid’s Lemma state when $p$ is not a prime?
What does Euclid’s Lemma state when $p$ is not a prime?
Signup and view all the answers
What is the significance of primes according to the text?
What is the significance of primes according to the text?
Signup and view all the answers
