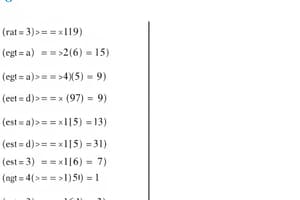Podcast
Questions and Answers
What is the primary rule regarding resources allowed during the exam?
What is the primary rule regarding resources allowed during the exam?
- Students may use notes as references.
- Calculators are encouraged for problem-solving.
- The exam is closed-book and no outside resources are allowed. (correct)
- Communication with peers is permissible.
How should a student handle a question they find difficult during the exam?
How should a student handle a question they find difficult during the exam?
- Skip it and move on without marking it.
- Mark it and return to it later. (correct)
- Attempt to solve it even if it takes a long time.
- Spend the entire time focusing on that question.
What is the total number of scoring points available in the exam?
What is the total number of scoring points available in the exam?
- 90 points, with no possibility of extra credit.
- 100 points, plus up to 10 points in extra credit. (correct)
- 110 points, totaling both the main exam and extra credit.
- 100 points, with an additional 5 points for extra credit.
How should students indicate they need extra space for their answers?
How should students indicate they need extra space for their answers?
What should students be cautious about when reading the exam questions?
What should students be cautious about when reading the exam questions?
What is the correct expression for the inductive step in proving P(n) by mathematical induction?
What is the correct expression for the inductive step in proving P(n) by mathematical induction?
If a task can be accomplished in either n1 ways or n2 ways, what is the total number of ways to complete the task?
If a task can be accomplished in either n1 ways or n2 ways, what is the total number of ways to complete the task?
How many different ways can a 5-letter password be chosen from 52 letters without repeating any letter?
How many different ways can a 5-letter password be chosen from 52 letters without repeating any letter?
How many one-to-one (injective) functions can be formed from a set A to itself if |A| = 5?
How many one-to-one (injective) functions can be formed from a set A to itself if |A| = 5?
How many bit strings of length 10 do not contain a consecutive sequence of 9 '1's?
How many bit strings of length 10 do not contain a consecutive sequence of 9 '1's?
What is the number of ways to choose an unordered team of 40 students from 89 registered students?
What is the number of ways to choose an unordered team of 40 students from 89 registered students?
In how many different ways can a committee of 3 members be formed from a group of 10 members?
In how many different ways can a committee of 3 members be formed from a group of 10 members?
What is the product rule in counting?
What is the product rule in counting?
What is the correct expression for S1 + S2?
What is the correct expression for S1 + S2?
Which type of progression does the sum of terms represent?
Which type of progression does the sum of terms represent?
If set A is countably infinite, which statement is true?
If set A is countably infinite, which statement is true?
What is the relationship between the cardinality of the sets Z and N?
What is the relationship between the cardinality of the sets Z and N?
What do the symbols in the expressions for S1 and S2 represent?
What do the symbols in the expressions for S1 and S2 represent?
How can one define the countable infinity of set A?
How can one define the countable infinity of set A?
What is the key difference between countably infinite and uncountably infinite sets?
What is the key difference between countably infinite and uncountably infinite sets?
In the context of set theory, what can be inferred about the cardinality of the natural numbers N?
In the context of set theory, what can be inferred about the cardinality of the natural numbers N?
Which formula correctly represents the sum of the first n positive integers?
Which formula correctly represents the sum of the first n positive integers?
How many different arrangements can three people have when seated around a circular table?
How many different arrangements can three people have when seated around a circular table?
What is the sum of the geometric series $1 + 2 + 4 + ... + 2^n$ for any non-negative integer n?
What is the sum of the geometric series $1 + 2 + 4 + ... + 2^n$ for any non-negative integer n?
What is a valid statement about the set of positive odd integers?
What is a valid statement about the set of positive odd integers?
What is the result of $1 + 2 + 2^2 + ... + 2^n$?
What is the result of $1 + 2 + 2^2 + ... + 2^n$?
Which concept is essential for proving the sum of the first n positive integers using induction?
Which concept is essential for proving the sum of the first n positive integers using induction?
Which of the following formulas is used for the sum of a finite geometric series?
Which of the following formulas is used for the sum of a finite geometric series?
How many bit strings of length 10 start with six 0s or end with five 0s?
How many bit strings of length 10 start with six 0s or end with five 0s?
Flashcards
Discrete Mathematics Exam II
Discrete Mathematics Exam II
A math exam covering discrete mathematics concepts.
Closed-book exam
Closed-book exam
An exam where students are not allowed to use books, notes, or other materials during the exam.
Multiple choice questions
Multiple choice questions
Questions with a set of possible answers, only one of which is correct.
Exam scoring
Exam scoring
Signup and view all the flashcards
Time management
Time management
Signup and view all the flashcards
Read all questions carefully
Read all questions carefully
Signup and view all the flashcards
Exam II
Exam II
Signup and view all the flashcards
Date of Exam II
Date of Exam II
Signup and view all the flashcards
S1 + S2 (part a)
S1 + S2 (part a)
Signup and view all the flashcards
S1 + S2 (part b)
S1 + S2 (part b)
Signup and view all the flashcards
S1 + S2 (part c)
S1 + S2 (part c)
Signup and view all the flashcards
Arithmetic Progression
Arithmetic Progression
Signup and view all the flashcards
Geometric Progression
Geometric Progression
Signup and view all the flashcards
Countably Infinite Set
Countably Infinite Set
Signup and view all the flashcards
Injection (A to N)
Injection (A to N)
Signup and view all the flashcards
Surjection (N to A)
Surjection (N to A)
Signup and view all the flashcards
Bijection
Bijection
Signup and view all the flashcards
|Z| vs |N| (Cardinality)
|Z| vs |N| (Cardinality)
Signup and view all the flashcards
Sum of first n natural numbers formula
Sum of first n natural numbers formula
Signup and view all the flashcards
Sum of a finite geometric series formula
Sum of a finite geometric series formula
Signup and view all the flashcards
Sum of the first n powers of 2
Sum of the first n powers of 2
Signup and view all the flashcards
Countably infinite set example
Countably infinite set example
Signup and view all the flashcards
Circular seating arrangements
Circular seating arrangements
Signup and view all the flashcards
Bit strings with specific prefixes/suffixes
Bit strings with specific prefixes/suffixes
Signup and view all the flashcards
Mathematical Induction - Inductive Step
Mathematical Induction - Inductive Step
Signup and view all the flashcards
Permutations (P(n,r))
Permutations (P(n,r))
Signup and view all the flashcards
Combinations (C(n,r))
Combinations (C(n,r))
Signup and view all the flashcards
Sum Rule
Sum Rule
Signup and view all the flashcards
Product Rule
Product Rule
Signup and view all the flashcards
One-to-one (Injective) Function
One-to-one (Injective) Function
Signup and view all the flashcards
Password Length Calculation
Password Length Calculation
Signup and view all the flashcards
Bit Strings - Consecutive 1's
Bit Strings - Consecutive 1's
Signup and view all the flashcards
Selecting a team of Students
Selecting a team of Students
Signup and view all the flashcards
Study Notes
Discrete Mathematics Exam II - Critical Information
- Exam Type: Closed-book
- Materials Allowed: No notes, internet, calculators, programs, or communication devices.
- Work Style: Work efficiently. If a problem is difficult, move on and come back to it later.
- Question Format: Read questions carefully. Expect variations and new combinations of previous homework questions.
- Continued Work: Use the back of previous pages or blank pages for additional space. Indicate the continuation with "continued" or "cont" and the problem number.
- Scoring: Exam is out of 100 points total, plus possible extra credit of 10 points.
- Multiple Choice: Multiple choice questions have only one correct answer. Numbers may differ from other exams.
Discrete Mathematics Exam II - Exam Questions
-
Question 1 (6 pts.): Σ (3⁰ + 2⁰) for integers n > 0
- Options (choose one): a) Σ (3⁰ + 2⁰) = (3+2)^n b) Σ (3⁰ + 2⁰) = Σ(3⁰) + Σ(2⁰) c) Σ (3⁰ + 2⁰) = (3 + 2) d) none of the above
-
Question 2 (6 pts.): Sum of terms (23^2 + 32^2)
- Options (choose one): a) arithmetic progression b) geometric progression c) both a and b d) none of the above
-
Question 3 (6 pts.): If set A is countably infinite
- Options (choose one): a) injection from A to set of natural numbers b) surjection from set of natural numbers to A c) bijection between A and set of natural numbers d) all of the above e) none of the above
-
Question 4 (6 pts.): Cardinality
- Options (choose one): a) If Z is uncountably infinite and N is countably infinite, |Z| > |N| b) If Z and N are both uncountably infinite, |Z| > |N| c) If Z and N are countably infinite, |Z| = |N| d) none of the above
-
Question 5 (6 pts.): Mathematical Induction
- Options (choose one): a) To prove P(n) by induction, prove k(P(k) => P(k+1)) b) P(1) => P(k) => P(k+1) => P(n) c) P(1) => for all k(P(k) => P(k+1)) => P(n) d) (P(1) ∧ (P(k) ∧ P(k+1)) => P(n))
-
Question 6 (6 pts.): Combining task possibilities. Given n₁ and n₂ task ways.
- Options (choose one): a) n₁ + n₂ by sum rule b) n₁ * n₂ by product rule c) n₁! * n₂! by product rule d) None of the above
-
Question 7 (6 pts.): Determine the number of possible 5-letter passwords using the English alphabet (case-sensitive). No letters can be repeated.
-
Question 8 (6 pts.): Number of one-to-one functions from set A to itself, where |A| = 5.
-
Question 9 (6 pts.): Bit strings of length 10 with no consecutive nines.
-
Question 10 (6 pts.): Number of ways to choose an unordered team of 40 students from 89 students.
Discrete Mathematics Exam II - Induction Proof
- Question 2.1: Prove by induction that 1+2+3+…+n = n(n+1)/2 for any integer n ≥ 1.
- Question 2.2: Prove by induction that 1+2^1+2^2+……+2^n = 2^(n+1)-1 for any integer n is ≥ 0
Discrete Mathematics Exam II - Counting
- Question 3.1: Is the set of positive odd integers countably infinite? Provide a function proof.
- Question 3.2: How many ways are there to seat three people around a circular table with three chairs?
- Question 3.3: How many bit strings of length 10 either begin with six 0s or end with five 0s (or both)?
Discrete Mathematics Exam II - Extra Credit
- Question 4: Prove the formula for the sum of a finite geometric progression. Use mathematical induction.
Studying That Suits You
Use AI to generate personalized quizzes and flashcards to suit your learning preferences.