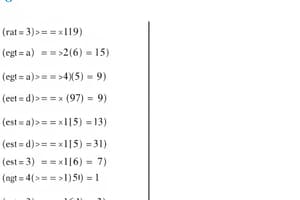Podcast
Questions and Answers
What key themes are emphasized in the approach to discrete mathematics?
What key themes are emphasized in the approach to discrete mathematics?
- Abstraction and the use of analogy in discovering new ideas.
- Structure and information as central concepts.
- Mathematical data being naturally “typed”.
- All of the above. (correct)
What is the role of algebraic reasoning in relation to mathematical structures?
What is the role of algebraic reasoning in relation to mathematical structures?
- It provides key insights into how structures are related. (correct)
- It is irrelevant to understanding the abstract nature of structures.
- It complicates the understanding of mathematical structures.
- It is only useful in continuous mathematics.
According to the provided information, what should mathematicians focus on to persuade others to accept a proposed solution?
According to the provided information, what should mathematicians focus on to persuade others to accept a proposed solution?
- Communicating the surface level solution.
- Communicating the result of their thinking. (correct)
- Communicating the reasoning and steps to a solution.
- The writing involved in an argument.
What is the standard for persuasion in mathematics?
What is the standard for persuasion in mathematics?
What should you consider a mathematical proof?
What should you consider a mathematical proof?
What does it mean if n is already at a certain stage?. (Assume that ( \frac{n}{d} ) is already in this stage)
What does it mean if n is already at a certain stage?. (Assume that ( \frac{n}{d} ) is already in this stage)
What does this text emphasize?
What does this text emphasize?
What does 3429 mean?
What does 3429 mean?
What is the purpose of introducing types of values such as letters in mathematics?
What is the purpose of introducing types of values such as letters in mathematics?
What is the meaning of the notation f(5) in mathematics, in one particular case?
What is the meaning of the notation f(5) in mathematics, in one particular case?
What does an algorithm convey?
What does an algorithm convey?
What is 'Our Earliest Mathematical Experience'?
What is 'Our Earliest Mathematical Experience'?
According to the information, what does a natural number express?
According to the information, what does a natural number express?
According to Vocabulary 1, what is successor?
According to Vocabulary 1, what is successor?
According to Postulate 1, what must all natural numbers be?
According to Postulate 1, what must all natural numbers be?
According to Postulate 2, what must all Predecessors be?
According to Postulate 2, what must all Predecessors be?
What is the reason why pred (0) would be nonsense?
What is the reason why pred (0) would be nonsense?
What does the symbol +: NX N → N indicate?
What does the symbol +: NX N → N indicate?
When evaluating an expression, how should parentheses be treated?
When evaluating an expression, how should parentheses be treated?
What must be decided for any new operation?
What must be decided for any new operation?
What is a monoid?
What is a monoid?
In the context of math, what is a 'commutative monoid'?
In the context of math, what is a 'commutative monoid'?
What is a 'group'?
What is a 'group'?
What is the role of the Axiom of Induction in proving the Identity Laws for addition?
What is the role of the Axiom of Induction in proving the Identity Laws for addition?
What does the basis of a proof aim to do?
What does the basis of a proof aim to do?
What is the purpose of proof tactics?
What is the purpose of proof tactics?
What does 'arbitrary' mean in the context of Proof Tactic 2?
What does 'arbitrary' mean in the context of Proof Tactic 2?
For statements in the form “if S then T”, what can you conclude from 'Direct Proof of an Implication?'
For statements in the form “if S then T”, what can you conclude from 'Direct Proof of an Implication?'
What should a proof by contraposition start with?
What should a proof by contraposition start with?
What is the result of postulates 1 and 2?
What is the result of postulates 1 and 2?
What can you say of two elements if they do not have a least element?
What can you say of two elements if they do not have a least element?
According to 'Pattern Matching' when can natural numbers be summarized?
According to 'Pattern Matching' when can natural numbers be summarized?
What does this mean: "every natural number matches exactly one of the two patterns"?
What does this mean: "every natural number matches exactly one of the two patterns"?
What is the most important thing for users of pattern matching to know?
What is the most important thing for users of pattern matching to know?
The conditions that guarantee termination and confluence are rather technical. What else can you say about them?
The conditions that guarantee termination and confluence are rather technical. What else can you say about them?
In the section titled 'Narrowing our pictures to actual counting', what is a flaw.
In the section titled 'Narrowing our pictures to actual counting', what is a flaw.
What does the lack of exercises do?
What does the lack of exercises do?
What is the primary goal of mathematicians regarding their work?
What is the primary goal of mathematicians regarding their work?
What is the primary focus when using careful mathematical notation and English?
What is the primary focus when using careful mathematical notation and English?
According to the information, what does discrete mathematics primarily focus on?
According to the information, what does discrete mathematics primarily focus on?
What provides a bridge between mathematics and computation?
What provides a bridge between mathematics and computation?
In the context of mathematical data, what is meant by 'typed'?
In the context of mathematical data, what is meant by 'typed'?
What does it mean to say that mathematics itself is ‘computational’?
What does it mean to say that mathematics itself is ‘computational’?
What is a crucial means of discovering new ideas and connecting existing knowledge?
What is a crucial means of discovering new ideas and connecting existing knowledge?
What is the purpose of formulaic writing in the early parts of a mathematical text?
What is the purpose of formulaic writing in the early parts of a mathematical text?
What key advantage can be realized through generalizing from particular instances?
What key advantage can be realized through generalizing from particular instances?
In the context of the text, what does an algorithm convey?
In the context of the text, what does an algorithm convey?
What does the text suggest about the role of the 'learner' when it comes to mechanical mathematical details like swapping between decimal and unary notation?
What does the text suggest about the role of the 'learner' when it comes to mechanical mathematical details like swapping between decimal and unary notation?
What does the basic vocabulary and the three postulates together aim to do?
What does the basic vocabulary and the three postulates together aim to do?
What is the goal of an inductive step in a proof employing induction?
What is the goal of an inductive step in a proof employing induction?
What does the proof tactic of Universal Generalization allow a mathematician to do?
What does the proof tactic of Universal Generalization allow a mathematician to do?
Which of the following is said of 'Pattern matching'?
Which of the following is said of 'Pattern matching'?
Which of the following illustrates how m \cdot (n + p) should be interpreted with parentheses?
Which of the following illustrates how m \cdot (n + p) should be interpreted with parentheses?
In math, what are the parts in an expression that should be evaluated earlier?
In math, what are the parts in an expression that should be evaluated earlier?
To know what precedence an operator will follow what must be decided?
To know what precedence an operator will follow what must be decided?
In an expression like m + n + p, what do we call the ability to decide what order the operations (or parentheses) ought to go?
In an expression like m + n + p, what do we call the ability to decide what order the operations (or parentheses) ought to go?
What does associativity do?
What does associativity do?
What is needed in order to make sense of new operations?
What is needed in order to make sense of new operations?
What is a monoid defined as?
What is a monoid defined as?
How does 'math your math teachers neglected to teach you' view discrete mathematics?
How does 'math your math teachers neglected to teach you' view discrete mathematics?
What characteristic defines the standards for persuasion in mathematics?
What characteristic defines the standards for persuasion in mathematics?
What is the significance of formulaic writing in the text, particularly in the earlier sections?
What is the significance of formulaic writing in the text, particularly in the earlier sections?
What is considered when determining the equality of two sets?
What is considered when determining the equality of two sets?
In the context of mathematical writing, why is it important to understand how a variable should be interpreted?
In the context of mathematical writing, why is it important to understand how a variable should be interpreted?
What does the text indicate as the purpose of using bold type face for certain words like 'waffles'?
What does the text indicate as the purpose of using bold type face for certain words like 'waffles'?
What is the meaning of calling the relation of being less or equal to 'defined' rather than 'algorithm'?
What is the meaning of calling the relation of being less or equal to 'defined' rather than 'algorithm'?
How does the text define the goal of 'induction' with the successor function??
How does the text define the goal of 'induction' with the successor function??
Why is it useful for some values in a math problem to be 'generic values'?
Why is it useful for some values in a math problem to be 'generic values'?
How many steps are most optimal to see if a calculation for a proof are obvious?
How many steps are most optimal to see if a calculation for a proof are obvious?
What exactly does the tactic with 'modus ponens' do?
What exactly does the tactic with 'modus ponens' do?
Why will most mathematicians try to follow a 'contrapositive' approach?
Why will most mathematicians try to follow a 'contrapositive' approach?
According to Postulate 3, what do natural numbers entail?
According to Postulate 3, what do natural numbers entail?
Why is it the most effective to "calculate" addition?
Why is it the most effective to "calculate" addition?
Why would a mathematician define any type of 'fixity?'
Why would a mathematician define any type of 'fixity?'
Why did Dr. Shuman tell congress that there is theory to back his claims?
Why did Dr. Shuman tell congress that there is theory to back his claims?
How would one show that m + n equals 0?
How would one show that m + n equals 0?
What should we as a reader have to assume to know 'properties' in the natural numbers?
What should we as a reader have to assume to know 'properties' in the natural numbers?
In the ''stepping stone' picture in order to satisfy the third axion, what is needed?
In the ''stepping stone' picture in order to satisfy the third axion, what is needed?
Why not refer to 0 being a 'positive number?'
Why not refer to 0 being a 'positive number?'
Flashcards
Discrete Mathematics
Discrete Mathematics
A broad area contrasting with continuous mathematics that focuses on structure and information.
Mathematical Proof
Mathematical Proof
A convincing argument, a genre of persuasive writing.
Natural Numbers
Natural Numbers
Numbers used to answer "How many are there?", including zero.
Successor
Successor
Signup and view all the flashcards
Algorithm
Algorithm
Signup and view all the flashcards
Precedence Rules
Precedence Rules
Signup and view all the flashcards
Infix Notation
Infix Notation
Signup and view all the flashcards
Prefix Notation
Prefix Notation
Signup and view all the flashcards
Postfix Notation
Postfix Notation
Signup and view all the flashcards
Binary Operation
Binary Operation
Signup and view all the flashcards
Associates to the left
Associates to the left
Signup and view all the flashcards
Associates to the right
Associates to the right
Signup and view all the flashcards
Recursion
Recursion
Signup and view all the flashcards
Law of Distribution
Law of Distribution
Signup and view all the flashcards
Commutative
Commutative
Signup and view all the flashcards
Associative
Associative
Signup and view all the flashcards
Zero identity
Zero identity
Signup and view all the flashcards
One identity
One identity
Signup and view all the flashcards
Non zero naturals
Non zero naturals
Signup and view all the flashcards
One and alone
One and alone
Signup and view all the flashcards
Monoid
Monoid
Signup and view all the flashcards
Commutative Monoid
Commutative Monoid
Signup and view all the flashcards
Robot with a Group
Robot with a Group
Signup and view all the flashcards
Require more
Require more
Signup and view all the flashcards
Study Notes
- The notes are based on "Contemporary Discrete Mathematics" by M. Andrew Moshier
Contemporary Discrete Mathematics
- Consists of many topics that contrast with continuous mathematics, like calculus.
- The sharp contrast between discrete and continuous mathematics is fictional and convenient only for syllabus organization
- Focuses on structure and information.
- The natural numbers and related inductive structures are central, providing a bridge between mathematics and computation.
- Emphasizes that mathematical data is naturally "typed," where natural numbers, real numbers, and polynomials constitute different data types.
- Stresses the Algebraic reasoning provides key insights into structural relationships
- Explores that mathematics itself is computational, using mathematical notation and English to convey information about structure.
- Abstraction and analogy are crucial for discovering new ideas and connecting existing knowledge.
Theorems and Persuasion
- Theorems are not about what one knows about square roots, but about explaining them
- Mathematicians spend time thinking about truth, then communicating these truths understandably.
- Standards for persuasion in mathematics are very high, aiming for "beyond any doubt" through convincing arguments called proofs.
Outline of this Book
- Explores the idea of counting things and its relationship to arithmetic.
- Investigates of putting things into lists, crucial for mathematics and base ten numerals.
- Covers foundational languages of contemporary mathematics: composition, sets, functions, and relations.
- Addresses questions about sets, functions, and relations, including what it means for two sets to be equal and how to specify particular sets.
- Investigates mathematical ideas, with emphasis on practical applications that either emerge from computing or are directly useful.
Notation Conventions
- Single letters as placeholders for values.
- Using letters from specific parts of the alphabet to refer to certain value types like using m, n, and p for natural numbers, and x, y, and z for generic values
- Symbols for names that are written in a bold type face
- algorithms refers to conveying a way of calculating something
- definitions refers to conveying a way to talk about something
Uses of Parentheses in Mathematics
- Function application, e.g., f(5) to apply the function f to the value 5
- Representing pairs and triples, e.g., (4,5) as an ordered pair
- Indicating ranges, e.g., (0,1) for real numbers strictly between 0 and 1
- Grouping sub-expressions
Natural Numbers
- Arithmetic on the natural numbers exhibits features of higher contemporary mathematics.
- An Informal definition of natural numbers: it amounts to answering a question "how many are there?"
- A natural number is a number that can be used to answer a how many question
Basic Vocabulary of Natural Numbers
- 0 is a special natural number
- Every natural number n, has a unique next natural number called a successor, denoted by n'
- N denotes the set of natural numbers
- Identifier n ranges over natural numbers, and write n ∈ N
Inductive Structures
- Postulate 1: Nothing Precedes 0; For every natural number n, it is the case that n' ≠ 0.
- Postulate 2: Predecessors are Unique; For any natural numbers m and n, if m' = n' then m = n.
- Definition 1: Predecessors and Positive Natural Numbers; For two natural numbers k and n, we say k is the predecessor of n if and only if n is the successor of k, that is, is k = n' A natural number m is positive if it has a predecessor.
- The Axiom of Induction is for “No Cheating"; Natural numbers cannot be invented.
- Vocabulary 1 is not enough and anything not in the vocabulary is not allowed as everything must be in the vocabulary
Basic Arithmetic Operations
- Addition works by counting ahead and can be calculated following a set of defined procedures
- Algorithm 1: Addition; The sum of m ∈ IN and n ∈ IN is a natural number m + n, calculated by the following:
- m+0=m
- m + k' = (m+k)' for any k ∈ N.
- Algorithm 2: Multiplication; The product of m ∈ IN and n ∈ /IN is a natural number m · n, calculated by the following;
- m.0=0
- m· k' = m+(m·k) for any k ∈ 𝙸N.
Precedence Rules
- Multiplications are evaluated before additions, superscripts are implicitly parenthesized, and successor notation has a high precedence.
- Infix: An operation is written in infix notation if it is written after its first operand. Standard arithmetic operations use infix notation: 5+4, 9-6, and so on.
- Prefix: An operation is written using prefix notation if it is written before all of its operands. such as trigonometric functions and max
- Postfix: An operation is written in postfix notation if it is written after all of its operands. for example: factorials
Associativity & Monoids
- It is important to decide whether to interpert whether is associates to the left or the right or whether something doesn't matter
- In summary, for any new operation, we need to decide if written in prefix, infix, or postfix notation, what it's precedence is or whether is is associates to the left or the right?
- Monoids: it is possible. to combine items associatively, and in which there is a “nothing” item that satisfies the identity laws.
- Robot Commands:
- abbreviaate the two basic robot commands by the letters f (move forward) and r (rotate 90 degrees clockwise)
- If sequencing is associative and has an identity element it is a monoid (do nothing)
Proofs
- Axiom of order helps to find relationships and reasoning that hold, proof employing the Axiom of Induction in this way is called a proof by simple arithmetic induction
- Tactics is a technique for proving assertions
- Proof Tactic 1: prove that all natural numbers have a certain property, to follow an outline
- Basis: Prove that 0 has the property.
- Inductive Hypothesis: Assume that k has the property for some (unspecified) k ∈ N.
- Inductive Step: Prove that k^ also has the property, using the inductive hypothesis as needed.
- Proof Tactic 1: prove that all natural numbers have a certain property, to follow an outline
- By the Axiom of Induction, everything holds for the natural numbers
Propositions
- Addition is associative (m+(n+p) = (m+n) + p)
- 0 is the identity for addition (in other words identity laws fro addition hold; 0 + m = m and m + 0 = m for all natural numbers m)
- Successors migrate in additions (meaning m+ n' = m' + n)
- Addition is commutative (means m+n=n + m)
- Addition is right cancellative (if m + p = n + p then m = n)
- A latin term is used to indicate "not"
- The following lemma is a restatement of something important!
- The symbol indicates the close of a proof
Proof Tactics
- To use an assertion that some property holds for some things(s), suppose that w is some particular object for which the assertion is true.
- Finding a Witness; it is often useful to provide a concrete thing with certain stated, but not necessarily obvious, properties.
- Use of Generic Values, or Universal Generalization: is to support that the hypothesis we were trying to satisfy is not dependent on which values were chosen for it
Ordering of the natural numbers
- Natural numbers may be pictured like stepping stones
- The stepping stone labelled ∗ has a unique predescessor because *` = * and Is + positive according to the definition
- To avoid this, it requires that no extra numbers are allowed
The Axiom of induction
- What the Vocabulary allows that which is not prohibited by the postulates is all
Division
- It doesn't always work
- We expect all that a-b=c ifand only if a=c+b exists
Monus
- Fix two natural numbers m and n, and consider the solutions of the inequality m ≤ x + n. Clearly, m is an example because m ≤ m + n.
- This operation is known by the obscure term monus
- Lemma 5: Addition is monotonic. - For any natural numbers, m, n, and p, if m ≤ n, then m + p n + p. Lemmma 6: Addition is order cancellative - For any natural numbers m, n and p, if m + p ≤ n + p, then m ≤ n.
Exponents
- Rising: easier to define
Lists
- An idea that is meant to be familiar
- List of "to do" items is a list
- Square brackets are used
- 5 cons [3,4} is [5,3,4]
Theorems
- For addition all we need know is that -Associative property holds - Identity laws fro addition hold - Successors migrate in additions
- An algorithm is what constitutes +
- with a set, then forms a monoid
Postulates
- 4 is to have no head or tail, and a list is not a head or a tail to have a known identifier
- 5 is the known uniqueness of head and tail
-For example know that [2,3,45.]= x,L then you have immediately also know two more thins-1 has a known predecesor
•So by the Axiom of induction, all natural numbers have the desired property.
Tactic
- Technique for proving assertions which uses an axion, which you yourself do use the original argument that have to satisfy certain postulates.
Lemma
- If the original process does not appear to be working what should we use instead
Examples of Recursion and Induction
Arithmetic operations on natural numbers are defined by recursion
- In this chapter is to look at several other operations that arise in applications, Some are very are quite familiar to you
- You many recall seeing it so we don't spell out and rules for stopping between decimal notations- we also dont spell out unnecessary parenthesis as those that are obvious
- To show 1+n= n' what needs to be determined 1st
Lists and Monoids
-If we can not reverse a robot command with and and it can't be equal to one, we see that what we can not work that way
-The main steps can never end if you say this is a process
-Suppose that you a pattern that you do have and what there is an assumption to a problem
+So by the axioms we use what should happen when there are to extra numbers
+Then prove and show that you were able to get the correct the solution
Basic Laws Of Arithmetic
-What they represent and be used where and so on
-When is it okay to give a value that is so and not
List Properties
-Length
-What if it is zero though
How lists interact with each other
-When two list have be able to combine to satisfy the equation-then this shows the definition
Laws
- The associative prop of a list
-How do show if it does and does not
What makes list valid
-If all items for both list agree
-It had an item where it must have
To give sense, they had an equality
Show if you were going to need a second solution
Studying That Suits You
Use AI to generate personalized quizzes and flashcards to suit your learning preferences.