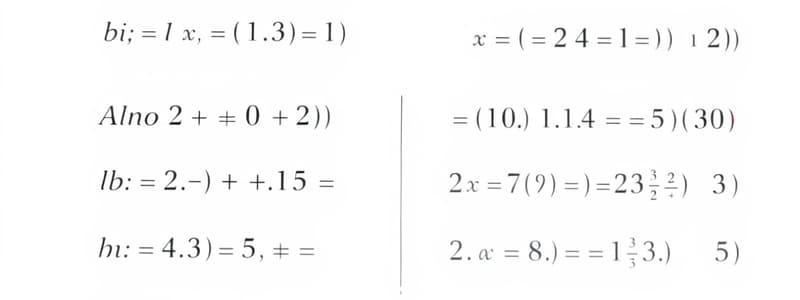Podcast
Questions and Answers
What is an absolute value equation?
What is an absolute value equation?
An equation that contains an absolute value expression, such as |X| = 4.
What are the solutions to the equation |X|=7?
What are the solutions to the equation |X|=7?
7 and -7
How do you solve the equation |X-3| = 8?
How do you solve the equation |X-3| = 8?
Rewrite it as X-3=8 or X-3=-8, leading to solutions x=11 or x=-5.
An OR case occurs when the inequality is set to be greater than.
An OR case occurs when the inequality is set to be greater than.
Signup and view all the answers
A Compound AND case occurs when the inequality is set to be greater than.
A Compound AND case occurs when the inequality is set to be greater than.
Signup and view all the answers
What needs to be checked to determine if an absolute value equation can be solved?
What needs to be checked to determine if an absolute value equation can be solved?
Signup and view all the answers
How do you solve the equation 3|2x-7|-5=4?
How do you solve the equation 3|2x-7|-5=4?
Signup and view all the answers
What is the first step in solving and graphing an inequality in one variable like -2x+3?
What is the first step in solving and graphing an inequality in one variable like -2x+3?
Signup and view all the answers
Study Notes
Absolute Value Equations
- Absolute value equation includes an expression like |X| = a, representing the distance of X from zero.
- An equation |X| = 4 has solutions X = 4 and X = -4.
Solving |X| = 7
- Solutions represent distances where X is 7 units away from zero, yielding X = 7 and X = -7.
Solving |X - 3| = 8
- Rewrite into two cases: X - 3 = 8 and X - 3 = -8.
- Solutions are X = 11 and X = -5, noted as an OR case due to two possible solutions.
OR Case Definition
- An OR case arises when an inequality is set to be less than, allowing multiple solutions.
Compound AND Case
- A Compound AND case occurs when the inequality is set to be greater than, leading to a single solution scenario.
Determining Solvability of Absolute Value Equations
- Absolute value expressions cannot equal negative numbers; if |X| = -a, there are no solutions.
- Isolate the absolute value expression first to assess solvability.
Solving 3|2x - 7| - 5 = 4
- Begin with the equation 3|2x - 7| - 5 = 4, then adjust to isolate the absolute value.
- Step-by-step isolation: add 5, divide by 3, yielding |2x - 7| = 3.
- Break into two cases: 2x - 7 = 3 and 2x - 7 = -3, leading to solutions X = 5 and X = 2.
Solving and Graphing Inequalities
- To solve and graph an inequality like -2x + 3, express the solution on a number line to visualize the inequality’s range.
Studying That Suits You
Use AI to generate personalized quizzes and flashcards to suit your learning preferences.
Description
Test your knowledge on absolute value equations with these flashcards from Chapter 6 of Algebra 1. Review definitions and solve equations involving absolute values to reinforce your understanding. Perfect for quick study sessions or exam preparation.
