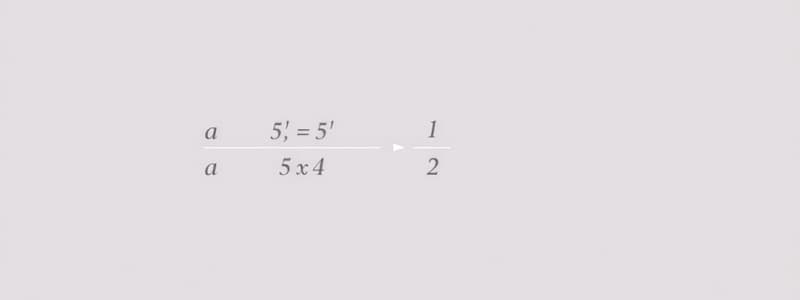Calculus: The Integral and Riemann Sums

Podcast

Play an AI-generated podcast conversation about this lesson

Questions and Answers

What is the primary purpose of a definite integral?

To find the roots of a function

To determine the area under the curve between two points (correct)

To find the maximum value of a function

To calculate the average value of a function

Which Riemann sum approximation method involves touching the function at the left corner of the rectangle?

Midpoint Riemann sum

Trapezoidal Riemann sum

Left Riemann sum (correct)

Right Riemann sum

How is the trapezoidal Riemann sum calculated?

(x2 - x1) * (f(x1) + f(x2))

(f(x2) + f(x1)) / 2 + Δx

(f(x2) + f(x1)) * Δx

(f(x2) + f(x1)) / 2 * Δx (correct)

What does the integral symbol '∫' represent?

The area under the curve of a function Signup and view all the answers

The antiderivative of the function $x^n$ is given by which formula?

$\frac{x^n+1}{n+1} + C$ Signup and view all the answers

What is the result of the integral ∫(1/x) dx?

ln|x| + C Signup and view all the answers

Which rule allows the evaluation of an integral in the form ∫[f(x) ± g(x)] dx?

Sum/difference rule Signup and view all the answers

When using long division for integration, which scenario necessitates this technique?

The degree of the numerator is greater than or equal to the degree of the denominator. Signup and view all the answers

What does the integral ∫(1/(x^2+1)) dx yield?

arctan(x) + C Signup and view all the answers

How can an improper integral be evaluated?

By substituting infinity with a large finite variable and taking the limit. Signup and view all the answers

If g(x) = ∫f(x) dx, what can be concluded about g'(x)?

g'(x) = f(x) Signup and view all the answers

Which method would be most appropriate to evaluate the integral ∫(2x + 3) / [(x - 3)(x + 3)] dx?

Partial fraction decomposition Signup and view all the answers

What happens to the area represented by an improper integral if the integral diverges?

The area is infinite. Signup and view all the answers

Which of the following statements is false regarding the indefinite integral ∫f(x) dx?

It cannot be expressed in terms of simple functions. Signup and view all the answers

What does the Fundamental Theorem of Calculus state about the relationship between differentiation and integration?

Integration reverses differentiation. Signup and view all the answers

Study Notes

The Integral

The definite integral is the area under the curve between two points on the x-axis (x = a and x = b).
The integral is the accumulation of change in the function between the two specified points.

Finding the Area

The Riemann sum uses rectangles to approximate the area under the curve.
Drawing more rectangles with the same width reduces the error between the estimated area and the actual area under the curve.
The limit definition of the integral is the limit as the number of rectangles approaches infinity of the sum of their areas.

Riemann Sums

The Riemann sum uses rectangles to approximate the area under the curve.
Left Riemann sum: Left corner of the rectangle touches the function.
Right Riemann sum: Right corner of the rectangle touches the function.
Midpoint Riemann sum: The middle of the rectangle touches the function. The formula for a midpoint Riemann sum is (x2 - x1)/2 + x1.
Trapezoidal Riemann sum: The left and right corner touches the function, drawing a straight line between them. The formula for a trapezoid Riemann sum is (f(x2) + f(x1))/2 * Δx.

Evaluating the Integral

The definite integral from A to B of f(x) dx is equal to the antiderivative of f(x) evaluated at B minus the antiderivative of f(x) evaluated at A.

Notation

The integral symbol is ∫.
The limits of integration are A and B, and the integrand is f(x).
dx represents an infinitesimally small change in x, and the entire expression is read as "the integral of f(x) with respect to x".
The definite integral is written in square brackets with the upper and lower limits of integration: [f(x)]^b_a.

Antiderivatives

The antiderivative of a function is the opposite operation of finding the derivative. It is also known as the indefinite integral.
The antiderivative of xⁿ is (xⁿ⁺¹)/(n+1) + C.
C is the constant of integration, which accounts for the fact that the derivative of a constant is always zero.

Antiderivative Rules

Anti-power rule: ∫x^a dx = x^a+1 / (a+1) + C
Integral of a constant: ∫a dx = ax + C
Constant multiple rule: ∫a * f(x) dx = a ∫ f(x) dx + C
Sum/difference rule: ∫[f(x) ± g(x)] dx = ∫f(x) dx ± ∫g(x) dx + C
Splitting bounds: ∫^c_a f(x) dx = ∫^b_a f(x) dx + ∫^c_b f(x) dx
Integral from a to a: ∫^a_a f(x) dx = 0
Flipping bounds: ∫^b_a f(x) dx = - ∫^a_b f(x) dx
Antiderivative of sine: ∫sin(x) dx = -cos(x) + C
Antiderivative of 1/x: ∫(1/x) dx = ln|x| + C
Antiderivative of 1/(x²+1): ∫[1/(x²+1)] dx = arctan(x) + C

Fundamental Theorem of Calculus

The indefinite integral ∫f(x) dx = F(x) + C, where F(x) is the antiderivative of f(x) and C is the constant of integration.
The derivative and integral are inverse operations: d/dx [∫f(x) dx] = f(x)

Fundamental Theorem of Calculus Graph Problem

If g(x) = ∫f(x) dx, then g'(x) = f(x).
When analyzing a graph of f(x), remember that you are looking at the derivative of g(x).
To find where g(x) has a relative maximum, find where f(x) (the derivative of g(x)) changes from positive to negative.
To find where g(x) is increasing, find where f(x) (the derivative of g(x)) is positive.

Integration Techniques

U-Substitution: Used for integrals where the integrand contains a function and its derivative.
- Identify a function u(x) and its derivative u'(x) in the integrand.
- Substitute u for the function, and du for its derivative.
- Evaluate the integral in terms of u.
- Substitute back u(x) to express the result in terms of x.
Long Division for Integration: Used for integrals where the integrand is a rational function with a numerator degree greater than or equal to the denominator degree.
- Perform long division on the rational function to simplify the expression.
- Integrate the simplified expression using known integration rules.
Integration by Completing the Square: Used for integrals containing quadratic expressions in the denominator.
- Complete the square for the quadratic expression in the denominator.
- Use trigonometric substitution or other techniques to evaluate the integral.
Integration by Parts: Used for integrals of products of two functions.
- Identify functions f(x) and g'(x) in the integrand.
- Use the integration by parts formula: ∫f(x)g'(x) dx = f(x)g(x) - ∫g(x)f'(x) dx.
- Evaluate the integral on the right side.
Integration by Partial Fraction Decomposition: Used for integrals containing rational functions with a denominator that can be factored into linear or quadratic factors.
- Decompose the rational function into a sum of simpler fractions.
- Integrate each simpler fraction using known integration rules.
- Combine the results to obtain the final integral.

Partial Fraction Decomposition

To integrate a rational function where the degree of the numerator is greater than or equal to the degree of the denominator, use partial fraction decomposition.
This involves factoring the denominator and expressing the rational function as a sum of simpler fractions with denominators that are the factors of the original denominator.
Partial fraction decomposition is a complex process that may require solving systems of equations.
An example is provided where the function (2x + 3) / (x - 3)(x + 3) is decomposed into (1.5) / (x- 3) + (0.5) / (x + 3)

Improper Integrals

An improper integral is a definite integral with one or both of its limits of integration as infinity.
Improper integrals cannot be evaluated directly, as infinity is not a number.
To evaluate an improper integral, use a limit to replace the infinite limit of integration with a finite variable and then evaluate the definite integral.
If the limit exists, the integral converges; otherwise, it diverges.
The integral of 1/x² from 5 to infinity is an example of an improper integral that converges to 1/5.
This means that the area under the curve of 1/x² from 5 to infinity is finite, even though the length of the interval is infinite.
The value of the improper integral represents the area under the curve between the specified bounds, even if one or both bounds are infinity.

Studying That Suits You

Use AI to generate personalized quizzes and flashcards to suit your learning preferences.

Description

This quiz covers the concepts of definite integrals and Riemann sums as methods for approximating the area under a curve. It explains the different types of Riemann sums and their applications in calculus. Test your understanding of these fundamental principles in integral calculus.