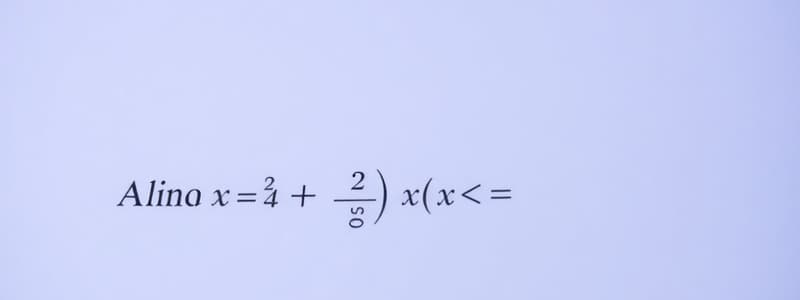Podcast
Questions and Answers
What is the formula to compute the average value of a continuous function over the interval [a, b]?
What is the formula to compute the average value of a continuous function over the interval [a, b]?
- $f_{avg} = (b - a) \cdot \int_a^b f(x) dx$
- $f_{avg} = \int_a^b f(x) dx$
- $f_{avg} = \frac{1}{b + a} \int_a^b f(x) dx$
- $f_{avg} = \frac{1}{b - a} \int_a^b f(x) dx$ (correct)
In the Mean Value Theorem for Integrals, what condition must the function f(x) satisfy on the interval [a, b]?
In the Mean Value Theorem for Integrals, what condition must the function f(x) satisfy on the interval [a, b]?
- f(x) must have a maximum value at a
- f(x) must be continuous on the interval (correct)
- f(x) must be differentiable on the entire interval
- f(x) must be continuous only at a
What can be inferred about the value of c in the Mean Value Theorem for Integrals?
What can be inferred about the value of c in the Mean Value Theorem for Integrals?
- c exists in [a, b] such that f(c) equals the average value of the function (correct)
- c does not exist within the interval [a, b]
- c is the average of a and b
- c is always greater than b
When determining the area between two curves y = f(x) and y = g(x) over an interval [a, b], which condition must be met?
When determining the area between two curves y = f(x) and y = g(x) over an interval [a, b], which condition must be met?
If f(t) = t^2 - 5t + 6cos(πt) on the interval [-1, 5/2], what is required to calculate its average value?
If f(t) = t^2 - 5t + 6cos(πt) on the interval [-1, 5/2], what is required to calculate its average value?
What is the primary purpose of calculating the average value of a function?
What is the primary purpose of calculating the average value of a function?
If f(x) = x^2 + 3x + 2, what is the first step to apply the Mean Value Theorem for Integrals on the interval [1, 4]?
If f(x) = x^2 + 3x + 2, what is the first step to apply the Mean Value Theorem for Integrals on the interval [1, 4]?
What does the integral $\int_a^b f(x) dx$ represent in the context of the Mean Value Theorem for Integrals?
What does the integral $\int_a^b f(x) dx$ represent in the context of the Mean Value Theorem for Integrals?
Flashcards
Average Function Value
Average Function Value
The average value of a continuous function f(x) over the interval [a, b] is calculated by integrating f(x) from a to b and dividing by (b-a).
Mean Value Theorem for Integrals
Mean Value Theorem for Integrals
For a continuous function f(x) on [a, b], there exists a number c in [a, b] such that the integral of f(x) from a to b is equal to f(c) times (b-a).
Area Between Two Curves
Area Between Two Curves
Area bounded between two curves (likely above the x-axis if unspecified in the problem) on a given interval. Calculate the integral of one function minus the other.
Continuous Function
Continuous Function
Signup and view all the flashcards
Integral
Integral
Signup and view all the flashcards
Interval [a, b]
Interval [a, b]
Signup and view all the flashcards
f(c)
f(c)
Signup and view all the flashcards
Finding c
Finding c
Signup and view all the flashcards
Study Notes
Average Function Value
- The average value of a continuous function f(x) over the interval [a, b] is calculated as:
- 1/(b-a) * ∫ab f(x) dx
Mean Value Theorem for Integrals
- If f(x) is continuous on [a, b], there exists a number c in [a, b] such that:
- ∫ab f(x) dx = f(c) * (b - a)
- This implies there's a point c within the interval where the function's value equals its average value.
- Simplified as: 1/(b-a) * ∫ab f(x) dx = f(c)
Area Between Curves
- Calculate the area between two curves y = f(x) and y = g(x) within the interval [a, b]. Assume f(x) ≥ g(x).
Studying That Suits You
Use AI to generate personalized quizzes and flashcards to suit your learning preferences.