Write the equation of the line in fully simplified slope-intercept form.

Understand the Problem

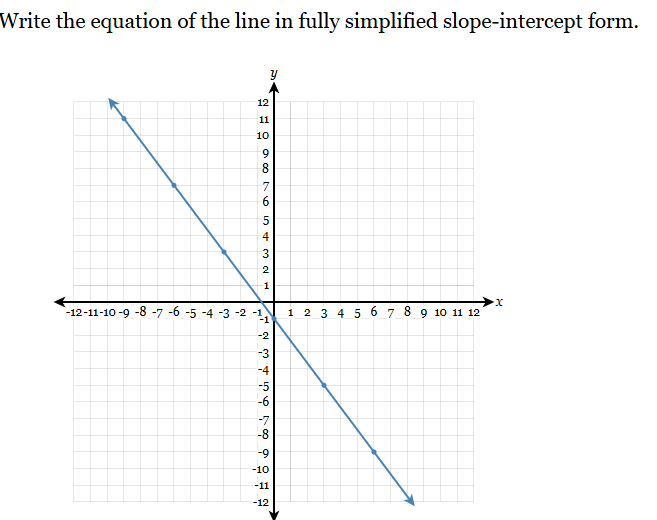
The question is asking for the equation of a given line on a graph, specifically in slope-intercept form, which is represented as y = mx + b, where m is the slope and b is the y-intercept. The task is to identify these values from the graph and write the equation accordingly.

Answer

The equation of the line is $$ y = -\frac{7}{4}x - \frac{19}{2} $$

Steps to Solve

Identify Two Points on the Line

From the graph, identify two clear points that lie on the line. For example:

Point A: (-10, 8)
Point B: (-2, -6)

Calculate the Slope (m)

Use the slope formula, which is given by:

$$ m = \frac{y_2 - y_1}{x_2 - x_1} $$

Substituting the points:

Let Point A be $(x_1, y_1) = (-10, 8)$ and Point B be $(x_2, y_2) = (-2, -6)$.

Thus,

$$ m = \frac{-6 - 8}{-2 - (-10)} = \frac{-14}{8} = -\frac{7}{4} $$

Find the Y-Intercept (b)

To find the y-intercept (b), use the slope-intercept form of the equation $y = mx + b$ and substitute one point and the slope.

Using Point A (-10, 8):

$$ 8 = -\frac{7}{4}(-10) + b $$

Calculating:

$$ 8 = 17.5 + b $$

Rearranging to find b:

$$ b = 8 - 17.5 = -9.5 $$

Write the Equation in Slope-Intercept Form

Substitute the values of m and b into the slope-intercept form equation:

$$ y = -\frac{7}{4}x - 9.5 $$

This is the equation of the line in fully simplified slope-intercept form.

The equation of the line in fully simplified slope-intercept form is

$$ y = -\frac{7}{4}x - \frac{19}{2} $$

More Information

The slope of the line is negative, indicating that as x increases, y decreases. The y-intercept shows where the line crosses the y-axis.

Tips

Confusing the points and calculating the slope incorrectly; always ensure you use the correct coordinates.
Mislabeling the y-intercept after finding it; double-check calculations and ensure you plug in the points correctly.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!