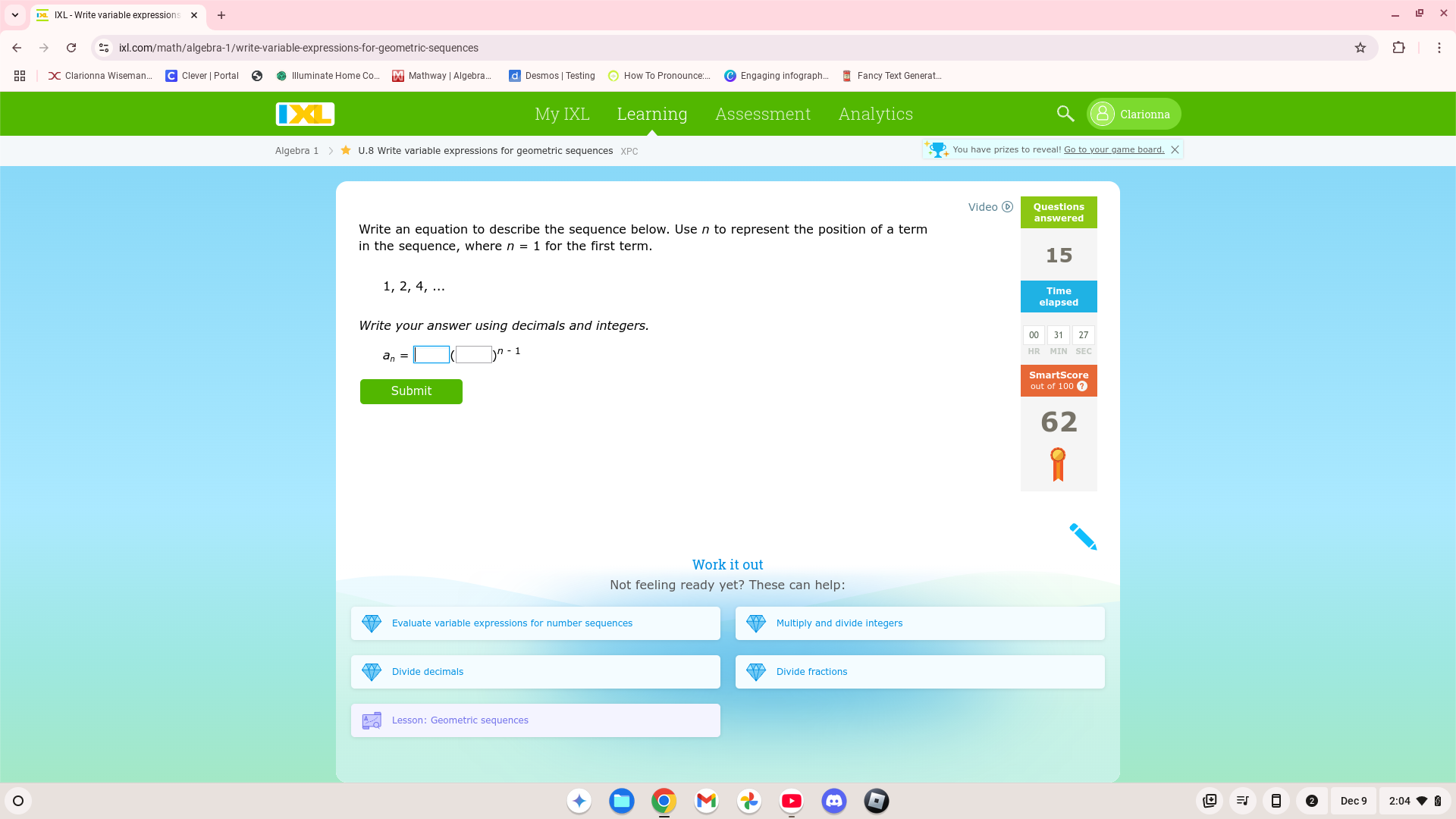
Write an equation to describe the sequence below. Use n to represent the position of a term in the sequence, where n = 1 for the first term. Sequence: 1, 2, 4, ... Write your answe... Write an equation to describe the sequence below. Use n to represent the position of a term in the sequence, where n = 1 for the first term. Sequence: 1, 2, 4, ... Write your answer using decimals and integers.
Understand the Problem
The question is asking to write an equation for a geometric sequence based on the given terms. Specifically, it's inquiring about how to express the terms of the sequence using a variable, n, where n indicates the position in the sequence starting from 1.
Answer
The expression for the \(n\)th term of the geometric sequence is \( a_n = 2^{n-1} \).
Answer for screen readers
The expression for the (n)th term of the geometric sequence is ( a_n = 2^{n-1} ).
Steps to Solve
- Identify the terms in the sequence
The given sequence is (1, 2, 4, \ldots). We can notice that the first term is (1), the second term is (2), and the third term is (4).
- Recognize the pattern of the sequence
Each term in the sequence is multiplied by (2) to get the next term. This indicates that the sequence is a geometric sequence with a common ratio.
- Determine the common ratio
The common ratio (r) can be calculated as follows:
- From (1) to (2): $$ r = \frac{2}{1} = 2 $$
- From (2) to (4): $$ r = \frac{4}{2} = 2 $$
Thus, the common ratio (r = 2).
- Write the general formula for the (n)th term
The formula for the (n)th term of a geometric sequence is given by: $$ a_n = a_1 \cdot r^{n-1} $$
Where:
- (a_1) is the first term ((1))
- (r) is the common ratio ((2))
- Substitute known values into the formula
Substituting the first term and common ratio into the formula: $$ a_n = 1 \cdot 2^{n-1} $$
- Finalize the expression
Thus, the final expression for the (n)th term of the sequence is: $$ a_n = 2^{n-1} $$
The expression for the (n)th term of the geometric sequence is ( a_n = 2^{n-1} ).
More Information
In geometric sequences, each term after the first is found by multiplying the previous term by a constant called the common ratio. In this case, the common ratio is (2), indicating that each term doubles the previous one. This type of sequence is useful in many areas of mathematics, including finance, computer science, and biology.
Tips
- Confusing geometric sequences with arithmetic sequences: Remember that in geometric sequences, you multiply to find the next term, whereas in arithmetic sequences, you add.
- Incorrectly identifying the common ratio: Ensure you're consistently checking the ratio between successive terms.
AI-generated content may contain errors. Please verify critical information