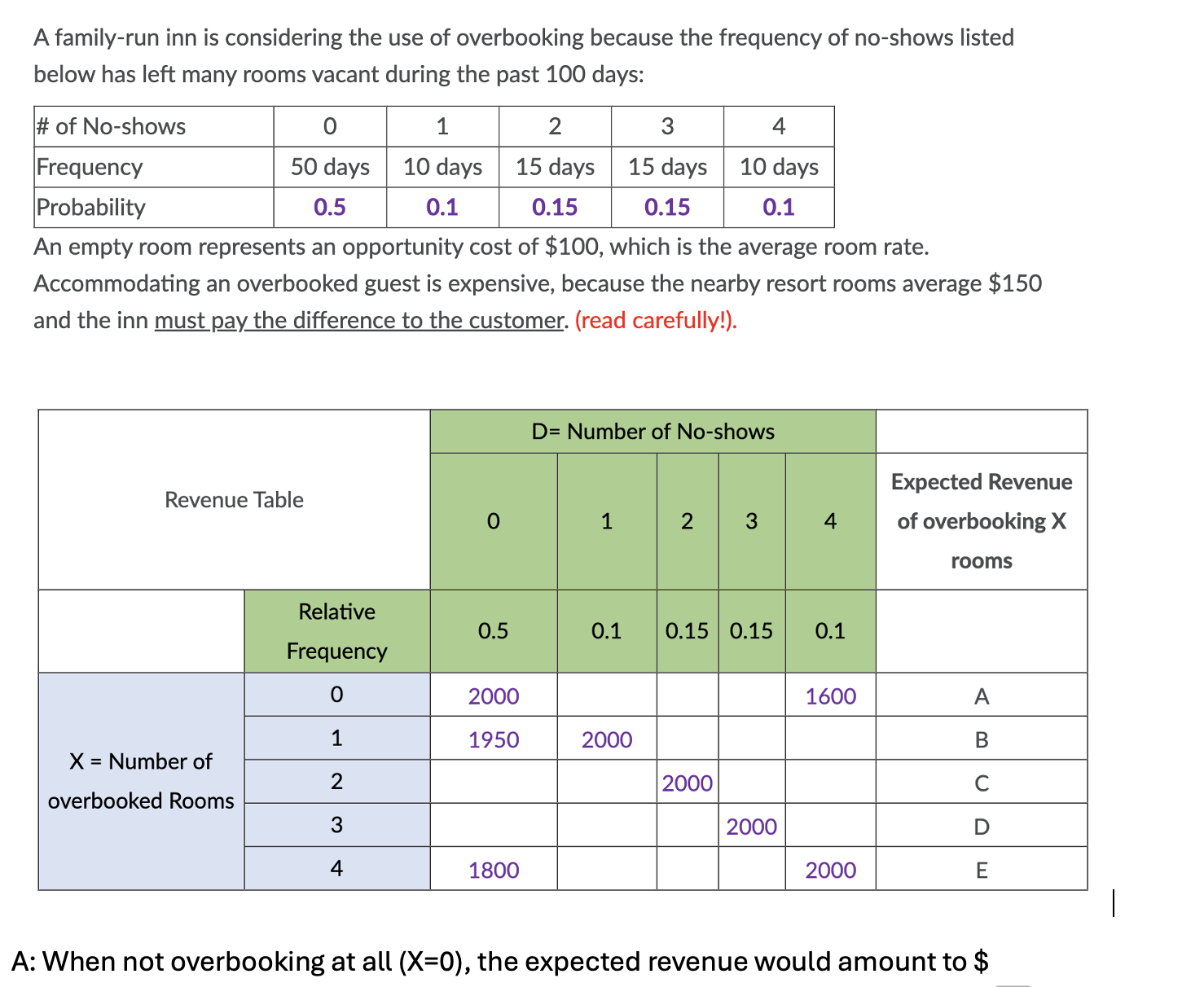
When not overbooking at all (X=0), the expected revenue would amount to $
Understand the Problem
The question is asking to calculate the expected revenue for a family-run inn when not overbooking at all (X=0) based on the provided data on no-shows. We need to analyze the given probabilities and frequencies to determine the expected revenue when zero rooms are overbooked.
Answer
The expected revenue when not overbooking at all (X=0) is $2000.
Answer for screen readers
When not overbooking at all (X=0), the expected revenue would amount to $2000.
Steps to Solve
-
Identify the relevant data for X=0 We know that when there are no rooms overbooked (X=0), we need to find the expected revenue using the no-show probabilities.
-
Revenue calculation for X=0 From the table, the expected revenue for X=0 is directly given as 2000. This is because they are not overbooking, and thus the revenue is based on how many guests show up against the available rooms.
-
Calculate Total Days Revenue The expected revenue can be simplified to just take the revenue from the actual no-shows. Since 50 days had no no-shows, the revenue would be: $$ \text{Revenue} = \text{Number of Rooms} \times \text{Room Rate} = 20 \times 100 = 2000 $$
When not overbooking at all (X=0), the expected revenue would amount to $2000.
More Information
The expected revenue of $2000 is based on the frequency data suggesting that on 50 days there were no no-shows, which maximized the occupancy and hence revenue.
Tips
- Confusing calculations involving no-shows with overbooking scenarios.
- Not recognizing that for X=0, the revenue is strictly from rooms available without any booking issues.
AI-generated content may contain errors. Please verify critical information