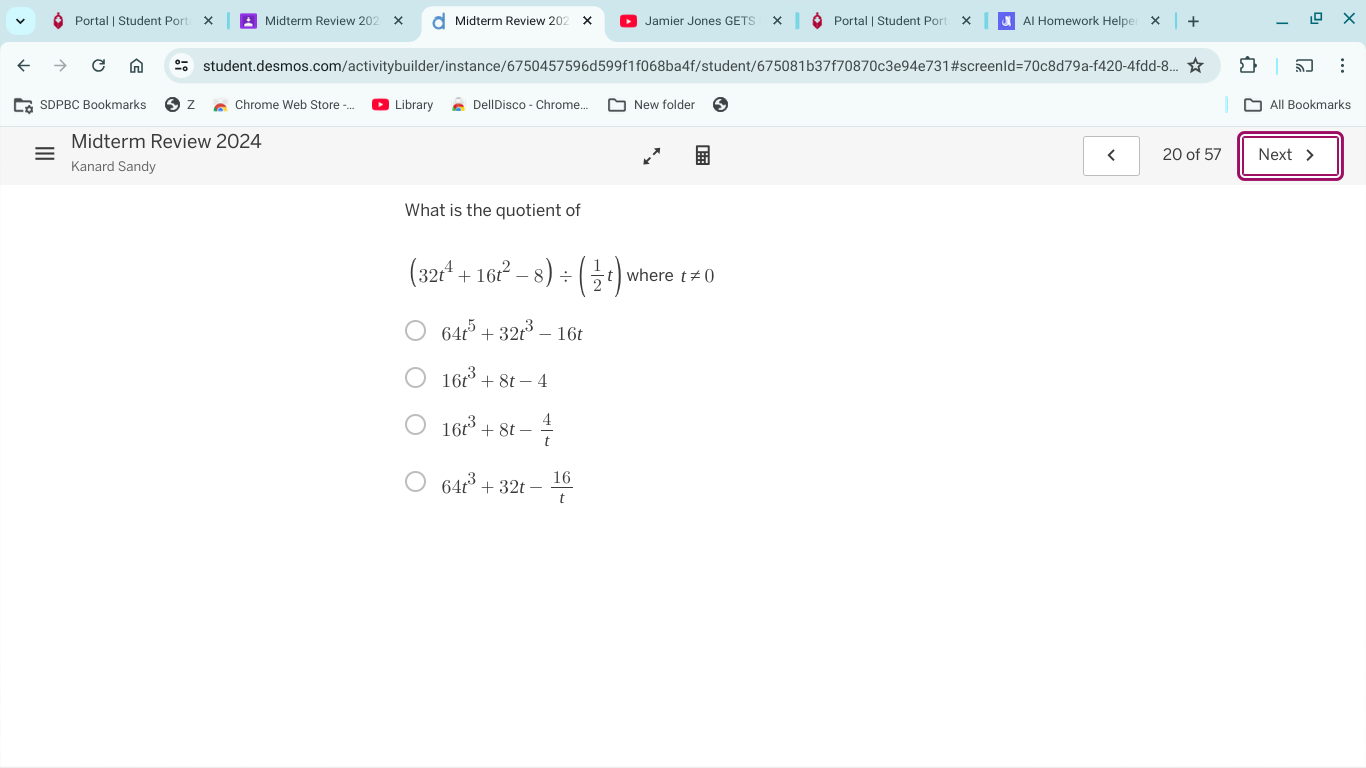
What is the quotient of (32t^4 + 16t^2 - 8) ÷ (1/2 * t) where t ≠ 0?
Understand the Problem
The question is asking for the result of dividing the polynomial expression (32t^4 + 16t^2 - 8) by (1/2 * t), where t cannot be zero. The goal is to find the quotient that results from this division.
Answer
The quotient is \(64t^3 + 32t - \frac{16}{t}\).
Answer for screen readers
The quotient is (64t^3 + 32t - \frac{16}{t}).
Steps to Solve
-
Rewrite the division expression
We need to divide the polynomial (32t^4 + 16t^2 - 8) by (\frac{1}{2}t). This can be rewritten as:
$$ \frac{32t^4 + 16t^2 - 8}{\frac{1}{2}t} $$
To simplify this division, we can multiply by the reciprocal of (\frac{1}{2}t):
$$ (32t^4 + 16t^2 - 8) \cdot \frac{2}{t} $$ -
Distribute the factor
Now distribute (\frac{2}{t}) to each term in the polynomial:
$$ = \frac{2 \cdot 32t^4}{t} + \frac{2 \cdot 16t^2}{t} - \frac{2 \cdot 8}{t} $$ -
Simplify each term
Now simplify each term:
- The first term:
$$ \frac{2 \cdot 32t^4}{t} = 64t^{4-1} = 64t^3 $$ - The second term:
$$ \frac{2 \cdot 16t^2}{t} = 32t^{2-1} = 32t $$ - The third term:
$$ \frac{2 \cdot 8}{t} = \frac{16}{t} $$
Putting it all together, we have:
$$ 64t^3 + 32t - \frac{16}{t} $$
The quotient is (64t^3 + 32t - \frac{16}{t}).
More Information
This result shows how polynomial division can be simplified using the reciprocal of the divisor. Notably, this process demonstrates the manipulation of polynomial expressions and highlights how terms with different degrees can interact.
Tips
- A common mistake is forgetting to multiply by the reciprocal of the divisor.
- Another mistake is miscalculating the powers of (t) during simplification.
AI-generated content may contain errors. Please verify critical information