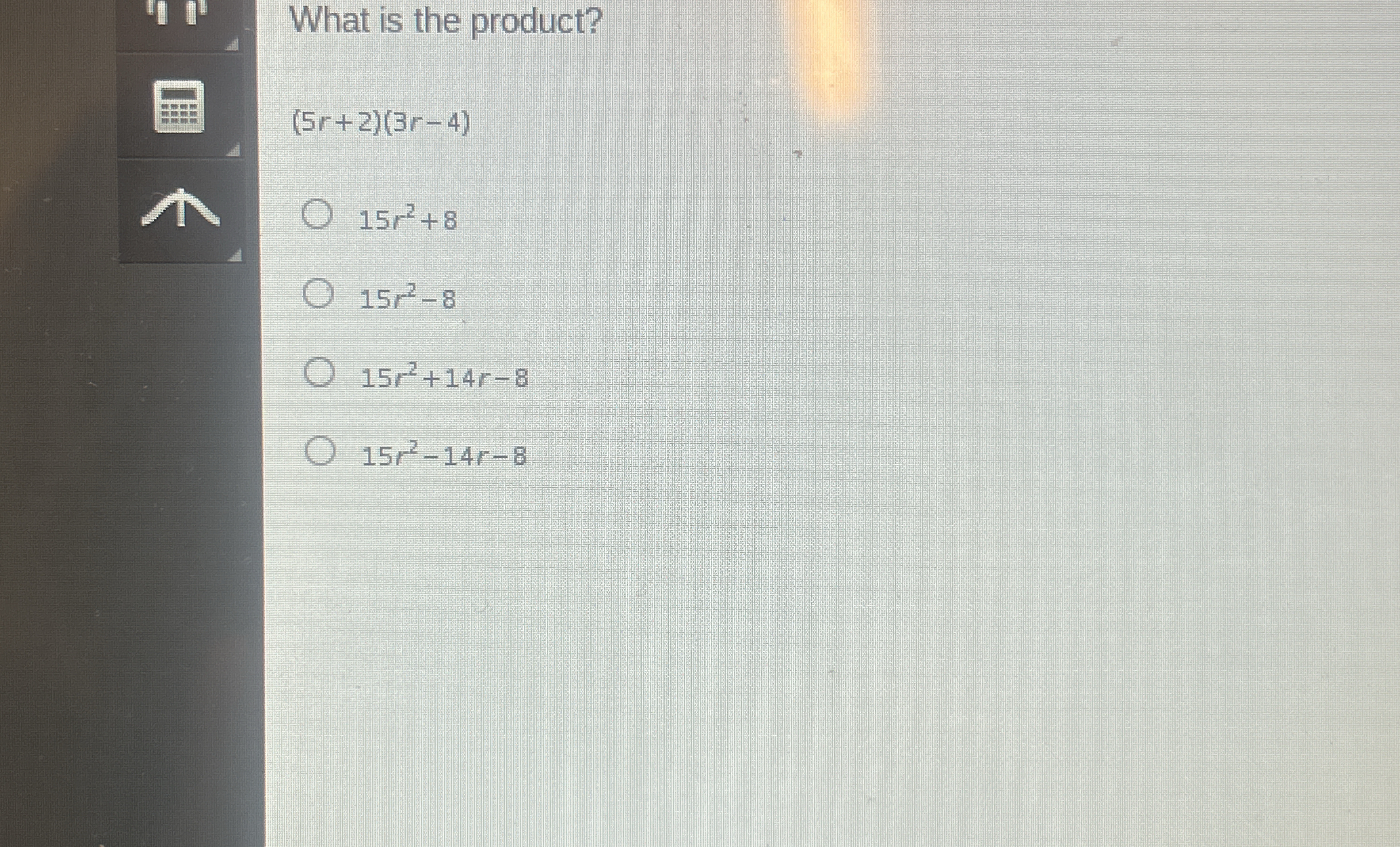
What is the product of (5r + 2)(3r - 4)?
Understand the Problem
The question is asking to multiply two binomials, (5r + 2) and (3r - 4), to find the product. The goal is to apply the distributive property to expand this expression.
Answer
The final product is $15r^2 - 14r - 8$.
Answer for screen readers
The product of $(5r + 2)(3r - 4)$ is:
$$ 15r^2 - 14r - 8 $$
Steps to Solve
-
Apply the distributive property
Distribute each term in the first binomial $(5r + 2)$ to each term in the second binomial $(3r - 4)$.
This results in:
$$ (5r)(3r) + (5r)(-4) + (2)(3r) + (2)(-4) $$ -
Calculate each multiplication
Now, compute each individual multiplication:
- $5r \cdot 3r = 15r^2$
- $5r \cdot -4 = -20r$
- $2 \cdot 3r = 6r$
- $2 \cdot -4 = -8$
-
Combine like terms
Next, combine the like terms:
- Combine $-20r$ and $6r$:
$$ -20r + 6r = -14r $$
Putting it all together, we have:
$$ 15r^2 - 14r - 8 $$
The product of $(5r + 2)(3r - 4)$ is:
$$ 15r^2 - 14r - 8 $$
More Information
The final expression represents the expanded form of the multiplication of two binomials. This process is commonly used in algebra for simplifying expressions.
Tips
- Forgetting to distribute every term in the first binomial to all terms in the second.
- Not combining like terms after performing the multiplications.
- Confusing signs during multiplication, particularly with negative numbers.
AI-generated content may contain errors. Please verify critical information