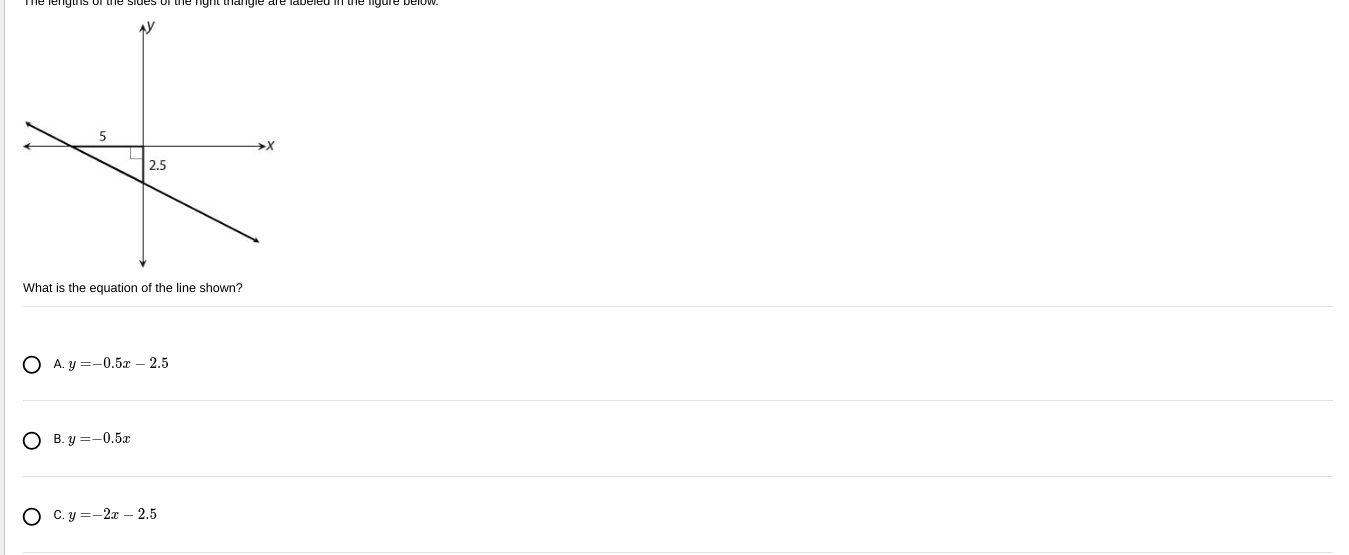
What is the equation of the line shown?

Steps to Solve

1. Identify the Coordinates of Key Points
   From the triangle provided, we can identify key points based on the right triangle's labeled side lengths. If we consider the right angle at the origin (0, 0), the points we can use are:

   • Point A at the origin (0, 0)
   • Point B at (2.5, 0) [horizontal side]
   • Point C at (0, 5) [vertical side]

2. Calculate the Slope of the Line
   The slope $m$ of a line passing through two points, $(x_1, y_1)$ and $(x_2, y_2)$, is calculated using the formula:
   $$ m = \frac{y_2 - y_1}{x_2 - x_1} $$
   Using points A (0, 0) and C (0, 5):

   • For the line through points A (0, 0) and B (2.5, 0): $$ m = \frac{0 - 5}{2.5 - 0} = \frac{-5}{2.5} = -2 $$

3. Use the Point-Slope Form to Find the Line's Equation
   The point-slope form of a line's equation is given as:
   $$ y - y_1 = m(x - x_1) $$
   We can use point A (0, 0):

   • Thus the equation becomes:
     $$ y - 0 = -2(x - 0) $$
   • Simplifying gives:
     $$ y = -2x $$

4. Rewrite the Equation in Slope-Intercept Form
   To express the line in slope-intercept form (which is $y = mx + b$), notice:

   • The slope is -2 and the y-intercept (b) is 0, hence:
     $$ y = -2x $$