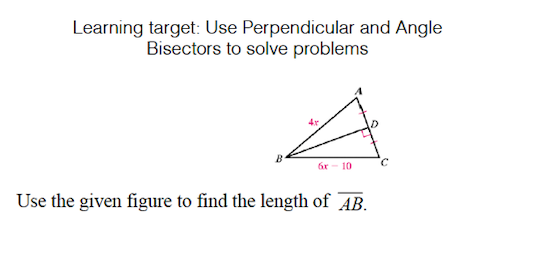
Use the given figure to find the length of AB.
Understand the Problem
The question is asking us to find the length of segment AB in the given figure, using the relationships between angle bisectors and perpendiculars. To solve it, we need to set up an equation based on the provided expressions for the lengths and solve for the variable r.
Answer
$$ AB = \frac{24r^2 - 40r}{10 - 4r} $$
Answer for screen readers
The length of segment (AB) is given by
$$ AB = \frac{24r^2 - 40r}{10 - 4r} $$
Steps to Solve
- Set up the equation based on the relationships given
From the figure, we know that segment (AD) is an angle bisector. Thus, we can state that:
$$ AD = AB \cdot \frac{AC}{AB + AC} $$
Given that (AD = 4r) and (AC = 6r - 10), we can express the relationship between (AB) and the segments.
- Express (AC) in terms of (AB)
Since (AD) bisects angle (A), by the Angle Bisector Theorem:
$$ \frac{AB}{AC} = \frac{AD}{AD} $$
This leads to substituting (AC) as follows:
$$ AC = AB + AD $$
- Substitute the values into the equation
Now substituting the known lengths into our relationship:
$$ 4r = AB \cdot \frac{6r - 10}{AB + (6r - 10)} $$
- Solve for (AB)
Rearrange the equation and solve for (AB):
Step 1: Multiply both sides by (AB + (6r - 10)):
$$ 4r (AB + (6r - 10)) = AB (6r - 10) $$
Step 2: Expand and rearrange:
$$ 4rAB + 24r^2 - 40r = 6rAB - 10AB $$
Step 3: Combine like terms:
$$ 10AB - 4rAB = 24r^2 - 40r $$
Step 4: Factor out (AB):
$$ AB(10 - 4r) = 24r^2 - 40r $$
Step 5: Solve for (AB):
$$ AB = \frac{24r^2 - 40r}{10 - 4r} $$
- Insert the value of (r) and calculate (AB)
After calculating (r), substitute back into the equation to find (AB).
The length of segment (AB) is given by
$$ AB = \frac{24r^2 - 40r}{10 - 4r} $$
More Information
This equation shows how the length of segment (AB) is related to the variable (r), which is determined by the dimensions from the angle bisector and provided lengths in the problem.
Tips
- Confusing the angle bisector theorem and triangle similarity; remember the ratios are based on segments created by the bisector.
- Not simplifying the equation fully; ensure no terms are left uncombined.
- Miscalculating variable substitutions; carefully verify each step when plugging in values.
AI-generated content may contain errors. Please verify critical information