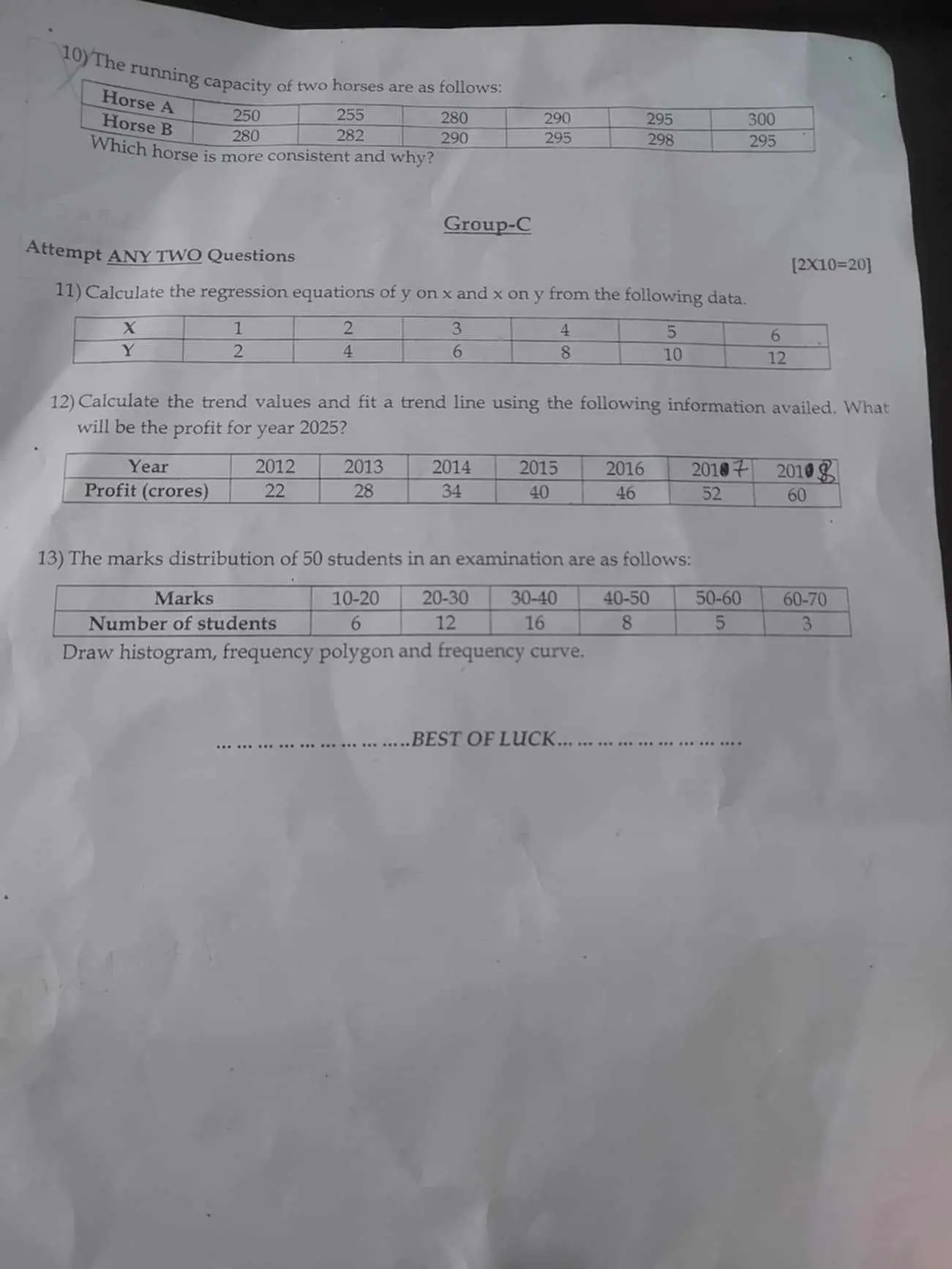
The running capacity of two horses are as follows: Horse A: 250, 255, 280, 290, 295, 300; Horse B: 280, 282, 290, 295, 298, 295. Which horse is more consistent and why? Calculate t... The running capacity of two horses are as follows: Horse A: 250, 255, 280, 290, 295, 300; Horse B: 280, 282, 290, 295, 298, 295. Which horse is more consistent and why? Calculate the regression equations of y on x and x on y from the following data: X: 1, 2, 3, 4, 5, 6; Y: 2, 4, 6, 8, 10, 12. Calculate the trend values and fit a trend line to find the profit for year 2025 from the given profit data for prior years. Draw a histogram, frequency polygon, and frequency curve for the marks distribution of 50 students in an examination. Read more

Steps to Solve

1. Calculate the Consistency of the Horses

To determine which horse is more consistent, we can calculate the standard deviation of the running capacities for each horse. The standard deviation indicates how much the values deviate from the mean.

For Horse A:

• Data: 250, 255, 280, 290, 295, 300
• Mean: $$ \text{Mean}_A = \frac{250 + 255 + 280 + 290 + 295 + 300}{6} = \frac{1670}{6} = 278.33 $$
• Variance: $$ \text{Variance}_A = \frac{(250 - 278.33)^2 + (255 - 278.33)^2 + (280 - 278.33)^2 + (290 - 278.33)^2 + (295 - 278.33)^2 + (300 - 278.33)^2}{6} = \frac{1841.11}{6} \approx 306.85 $$
• Standard Deviation: $$ \text{SD}_A = \sqrt{306.85} \approx 17.53 $$

For Horse B:

• Data: 280, 282, 290, 295, 298, 295
• Mean: $$ \text{Mean}_B = \frac{280 + 282 + 290 + 295 + 298 + 295}{6} = \frac{1740}{6} = 290 $$
• Variance: $$ \text{Variance}_B = \frac{(280 - 290)^2 + (282 - 290)^2 + (290 - 290)^2 + (295 - 290)^2 + (298 - 290)^2 + (295 - 290)^2}{6} = \frac{84}{6} = 14 $$
• Standard Deviation: $$ \text{SD}_B = \sqrt{14} \approx 3.74 $$

2. Determining Consistency

The horse with the lower standard deviation is more consistent. Since $$ \text{SD}_A \approx 17.53 \quad \text{and} \quad \text{SD}_B \approx 3.74 $$ we conclude that Horse B is more consistent than Horse A.