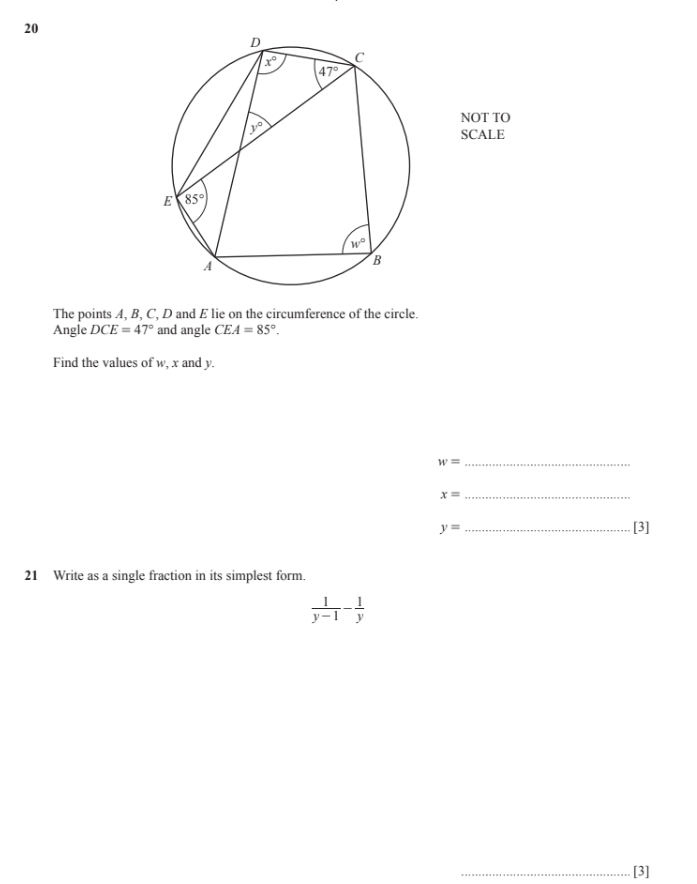
The points A, B, C, D and E lie on the circumference of the circle. Angle DCE = 47° and angle CEA = 85°. Find the values of w, x and y.
Understand the Problem
The problem involves finding the values of angles w, x, and y in a circle, given that points A, B, C, D, and E lie on the circumference. You are provided with the measures of angle DCE which is 47 degrees and angle CEA which is 85 degrees. Using circle theorems, we can determine missing angles.
Answer
$w = 85^\circ$ $x = 47^\circ$ $y = 48^\circ$
Answer for screen readers
$w = 85^\circ$ $x = 47^\circ$ $y = 48^\circ$
Steps to Solve
-
Find angle $w$ Angle $w$ ($ \angle ABC $) subtends the same arc, $AC$, as angle $ \angle CEA $. Therefore, $w = 85^\circ$ because angles subtended by the same arc are equal.
-
Find angle $x$ Angle $x$ ($ \angle CDA $) subtends the same arc, $AE$, as angle $ \angle ACE $. $ \angle ACE = \angle DCE = 47^\circ$. Therefore, $x = 47^\circ$ since angles subtended by the same arc are equal.
-
Find angle $y$ Consider quadrilateral $CDEA$. The sum of opposite angles in a cyclic quadrilateral is $180^\circ$. Therefore, $ \angle CEA + \angle CDA = 180^\circ$. We are given that $\angle CEA = 85^\circ$ and we found that $\angle CDA = x + y = 47^\circ $. So we have $\angle CDE = 47^\circ$. Given that the whole angle $\angle CDE = x + y $, this gives $ \angle CEA + (\angle CDE + \angle y) = 180 $. However, the sum of the angles $\angle DCE + \angle CEA + \angle EDC = 180^\circ$ is $180^\circ$, $47^\circ + 85^\circ + \angle EDC = 180^\circ$ $\angle EDC = 180^\circ - 47^\circ - 85^\circ = 48^\circ$. Thus $y =48^\circ$.
$w = 85^\circ$ $x = 47^\circ$ $y = 48^\circ$
More Information
The "angles in the same segment are equal" theorem is crucial for finding angles that subtend the same arc on the circumference of a circle; this is how we could derive $w$ and $x$. Also, the sum of opposite angles in a cyclic quadrilateral equals $180^\circ$; this wasn't directly used.
Tips
A common mistake is to incorrectly identify which angles subtend the same arc, or to confuse angles in the same segment with other angle relationships in circles. Another mistake could be messing up the angle chasing (adding and subtracting angles) to arrive at the correct answer.
AI-generated content may contain errors. Please verify critical information