The endpoints of CD are C(-2, 9) and D(3, -1). Find the coordinates of the midpoint M.
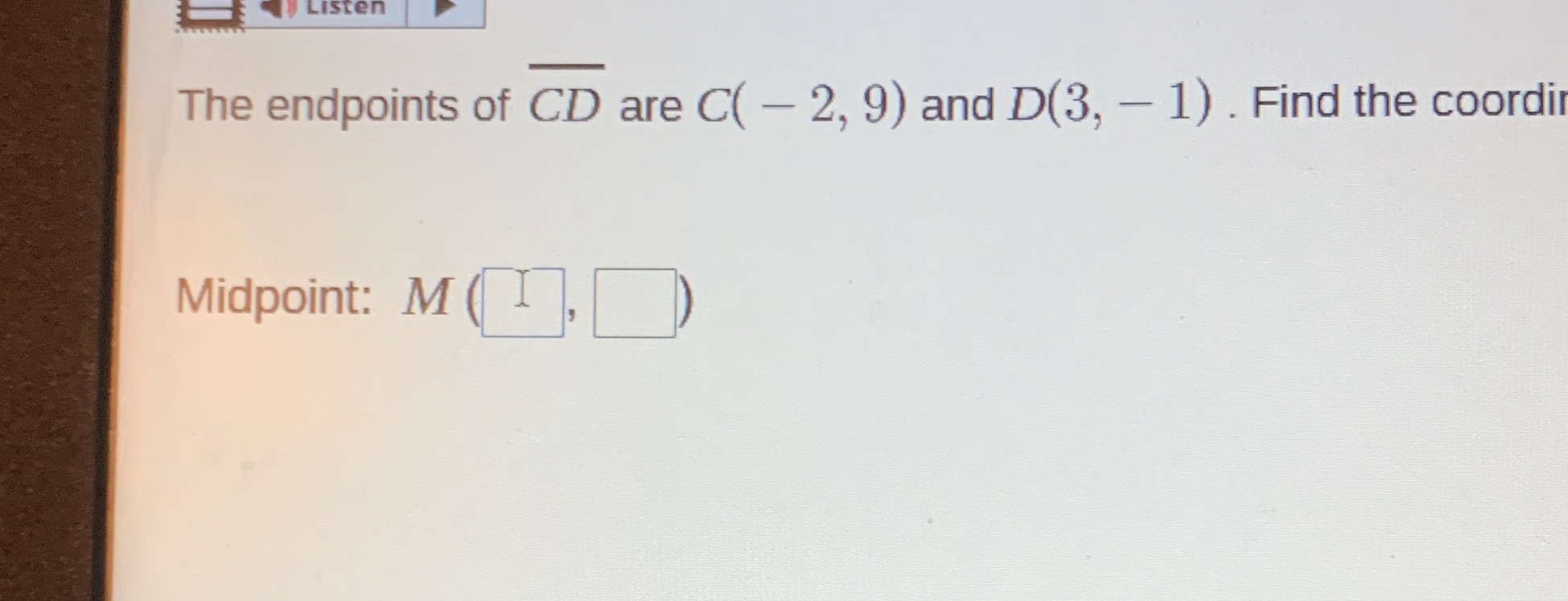
Understand the Problem
The question is asking to find the midpoint of a line segment defined by endpoints C and D using their coordinates. This involves applying the midpoint formula, which averages the x-coordinates and y-coordinates of the endpoints.
Answer
The midpoint is $M(0.5, 4)$.
Answer for screen readers
The coordinates of the midpoint $M$ are $(0.5, 4)$.
Steps to Solve
- Identify the Coordinates of Points C and D
The coordinates for point C are $(-2, 9)$ and for point D are $(3, -1)$.
- Apply the Midpoint Formula
The midpoint $M$ of a line segment defined by endpoints $(x_1, y_1)$ and $(x_2, y_2)$ can be calculated using the formula: $$ M = \left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right) $$
- Substitute the Values into the Formula
Here, $(x_1, y_1) = (-2, 9)$ and $(x_2, y_2) = (3, -1)$. Substitute these values into the formula: $$ M = \left(\frac{-2 + 3}{2}, \frac{9 + (-1)}{2}\right) $$
- Calculate the x-coordinate of the Midpoint
First, calculate the x-coordinate: $$ \frac{-2 + 3}{2} = \frac{1}{2} = 0.5 $$
- Calculate the y-coordinate of the Midpoint
Next, calculate the y-coordinate: $$ \frac{9 + (-1)}{2} = \frac{8}{2} = 4 $$
- State the Coordinates of the Midpoint
The coordinates of the midpoint $M$ are: $$ M(0.5, 4) $$
The coordinates of the midpoint $M$ are $(0.5, 4)$.
More Information
The midpoint formula is useful for finding the exact center point of a segment defined by two endpoints in a coordinate system. Midpoints can help in various applications like geometry and navigation.
Tips
- Forgetting to average both x and y coordinates can lead to incorrect midpoint values. Always ensure both sets of coordinates are included in the calculation.
- Confusing the signs when one of the coordinates is negative. Double-check arithmetic operations to avoid errors.
AI-generated content may contain errors. Please verify critical information