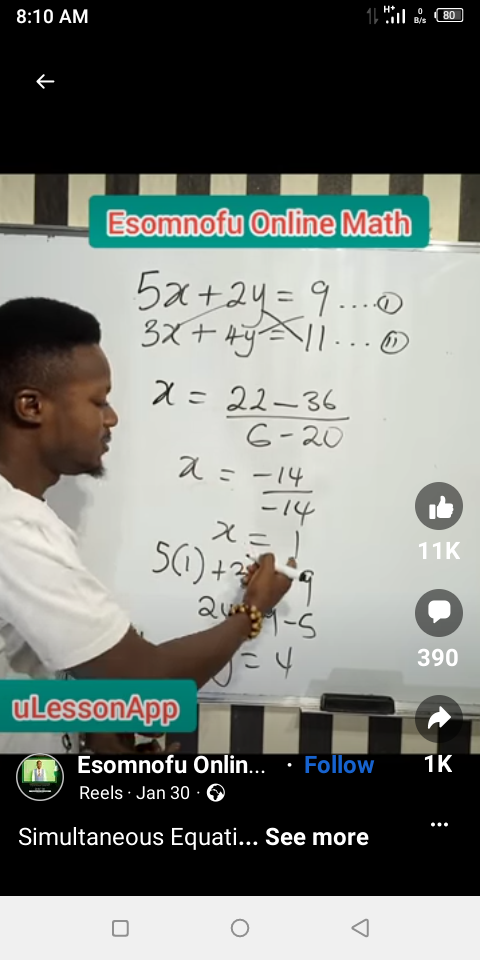
Solve the simultaneous equations: 5x + 2y = 9 and 3x + 4y = 11.
Understand the Problem
The question involves solving a system of simultaneous equations. It presents two equations and seeks to find the values of the variables involved, namely x and y. The approach would typically include methods such as substitution or elimination to determine the values of these variables.
Answer
The solution is $x = 1$, $y = 2$.
Answer for screen readers
The solution to the system of equations is:
$$ x = 1, ; y = 2 $$
Steps to Solve
-
Identify the equations
The given equations are:
$$ 5x + 2y = 9 \quad (1) $$
$$ 3x + 4y = 11 \quad (2) $$ -
Choose a method
We'll use the elimination method to solve the system of equations. -
Multiply to align coefficients
To eliminate one variable, we can multiply the entire first equation by 2 and the second equation by 1 so that the coefficients of $y$ will be the same when subtracted:
$$ 2(5x + 2y) = 2(9) \implies 10x + 4y = 18 \quad (3) $$
$$ 3x + 4y = 11 \quad (2) $$ -
Subtract the new equations
Now subtract equation (2) from equation (3):
$$ (10x + 4y) - (3x + 4y) = 18 - 11 $$
This simplifies to:
$$ 7x = 7 $$ -
Solve for x
Now divide both sides by 7 to find $x$:
$$ x = 1 $$ -
Substitute x back into one equation
Substitute $x = 1$ into equation (1):
$$ 5(1) + 2y = 9 $$
This simplifies to:
$$ 5 + 2y = 9 $$ -
Solve for y
Now, isolate $y$:
$$ 2y = 9 - 5 $$
$$ 2y = 4 $$
$$ y = 2 $$
The solution to the system of equations is:
$$ x = 1, ; y = 2 $$
More Information
The solution represents the point of intersection of the two lines represented by the equations. This means that at $x = 1$ and $y = 2$, both equations are satisfied simultaneously.
Tips
- Incorrect coefficients: When multiplying the equations, sometimes incorrect coefficients can lead to errors. Always double-check the multiplication.
- Sign errors: Be careful with addition and subtraction steps, especially when working with negative signs.
AI-generated content may contain errors. Please verify critical information