Solve the following quadratic equation for all values of x in simplest form: 3(x - 7)² + 16 = 46.
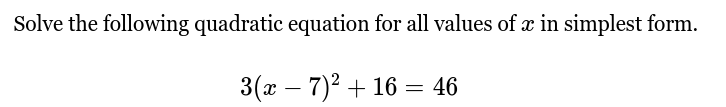
Understand the Problem
The question is asking to solve the quadratic equation given in the form of 3(x - 7)² + 16 = 46 for all possible values of x, and to present the solutions in their simplest form.
Answer
The solutions are \( x = 7 + \sqrt{10} \) and \( x = 7 - \sqrt{10} \).
Answer for screen readers
The solutions to the equation are ( x = 7 + \sqrt{10} ) and ( x = 7 - \sqrt{10} ).
Steps to Solve
- Isolate the quadratic term
Subtract 16 from both sides of the equation to isolate the term with the square:
$$ 3(x - 7)² + 16 - 16 = 46 - 16 $$
This simplifies to:
$$ 3(x - 7)² = 30 $$
- Divide by the coefficient
Next, divide both sides by 3 to simplify further:
$$ \frac{3(x - 7)²}{3} = \frac{30}{3} $$
This results in:
$$ (x - 7)² = 10 $$
- Take the square root
Take the square root of both sides. Remember to consider both the positive and negative roots:
$$ x - 7 = \pm \sqrt{10} $$
- Solve for (x)
Add 7 to both sides to solve for (x):
$$ x = 7 \pm \sqrt{10} $$
This gives us two possible solutions for (x):
$$ x = 7 + \sqrt{10} \quad \text{and} \quad x = 7 - \sqrt{10} $$
The solutions to the equation are ( x = 7 + \sqrt{10} ) and ( x = 7 - \sqrt{10} ).
More Information
When solving quadratic equations, the method of completing the square is particularly useful. Here, ( \sqrt{10} ) is an irrational number, so the solutions are expressed in their simplest form rather than as decimal approximations.
Tips
- Not isolating the quadratic term first: It's important to isolate the square before taking the square root.
- Forgetting the ± sign when taking square roots: Remember that both positive and negative roots must be considered.
AI-generated content may contain errors. Please verify critical information