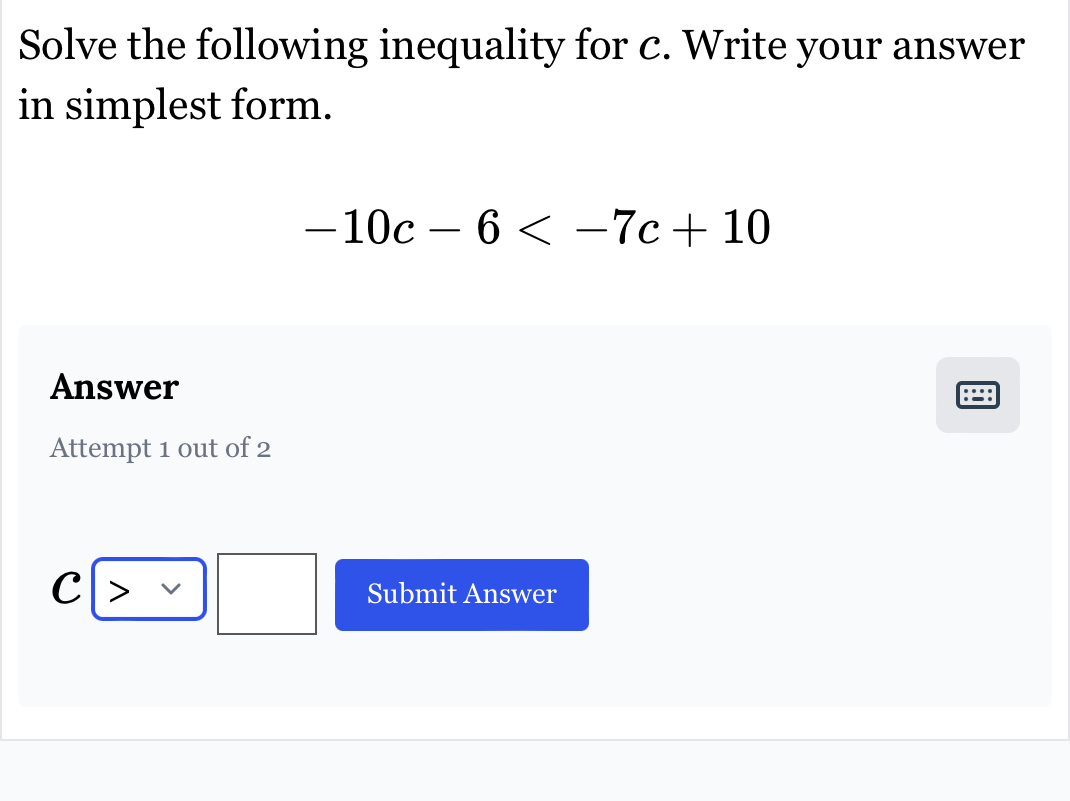
Solve the following inequality for c: -10c - 6 < -7c + 10. Write your answer in simplest form.
Understand the Problem
The question is asking us to solve the inequality for the variable 'c'. This involves isolating 'c' on one side of the inequality while following the rules of algebra for inequalities.
Answer
$$ c > \frac{-16}{3} $$
Answer for screen readers
The solution to the inequality is
$$ c > \frac{-16}{3} $$
Steps to Solve
- Combine like terms on the left side
Starting with the inequality:
$$ -10c - 6 < -7c + 10 $$
We can add (10c) to both sides to move the terms involving (c):
$$ -6 < 3c + 10 $$
- Isolate the term with 'c'
Next, subtract (10) from both sides to isolate the term with (c):
$$ -6 - 10 < 3c $$
This simplifies to:
$$ -16 < 3c $$
- Solve for 'c' by dividing
Now, divide both sides by (3) to solve for (c):
$$ \frac{-16}{3} < c $$
Or, rearranging:
$$ c > \frac{-16}{3} $$
The solution to the inequality is
$$ c > \frac{-16}{3} $$
More Information
The solution indicates that (c) must be greater than approximately (-5.33). In terms of practical applications, this can be used in contexts where certain quantities need to exceed a threshold.
Tips
- Not reversing the inequality sign when multiplying or dividing by a negative number (not applicable here).
- Forgetting to combine like terms properly before isolating the variable.
AI-generated content may contain errors. Please verify critical information