Put the quadratic into vertex form and state the coordinates of the vertex: y = x^2 + 2x + 17.
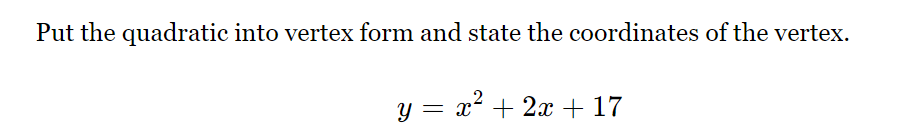
Understand the Problem
The question is asking to convert the given quadratic equation into vertex form and identify the coordinates of its vertex. This involves completing the square for the quadratic expression provided.
Answer
The vertex form is $y = (x + 1)^2 + 16$ and the vertex coordinates are $(-1, 16)$.
Answer for screen readers
The vertex form of the quadratic is
$$ y = (x + 1)^2 + 16 $$
The coordinates of the vertex are $(-1, 16)$.
Steps to Solve
- Identify the quadratic expression
The given quadratic equation is
$$ y = x^2 + 2x + 17 $$
- Extract the quadratic and linear terms
From the equation, identify the terms related to $x$:
$$ y = (x^2 + 2x) + 17 $$
- Complete the square
To complete the square for the expression $x^2 + 2x$, take half of the coefficient of $x$, square it, and add it inside the parentheses. The coefficient is 2, so half is 1, and squaring it gives 1.
Add and subtract this square inside the expression:
$$ y = (x^2 + 2x + 1 - 1) + 17 $$
- Rewrite the expression
This can be rewritten as:
$$ y = (x + 1)^2 - 1 + 17 $$
Combine the constant terms:
$$ y = (x + 1)^2 + 16 $$
- Identify the vertex
The vertex form of a quadratic is given by
$$ y = a(x - h)^2 + k $$
From our equation,
$$ y = (x + 1)^2 + 16 $$
We can deduce that $(h, k) = (-1, 16)$, which gives the vertex coordinates.
The vertex form of the quadratic is
$$ y = (x + 1)^2 + 16 $$
The coordinates of the vertex are $(-1, 16)$.
More Information
The vertex form of a quadratic equation easily allows you to identify the vertex of the parabola. The vertex represents the minimum or maximum point of the quadratic function, depending on the direction of the parabola. In this case, since the coefficient of the squared term is positive, the vertex is a minimum point.
Tips
- Forgetting to adjust the constant: When completing the square, it's important to add and then immediately subtract the squared value inside the expression to keep the equation balanced.
- Incorrectly identifying the vertex: Ensure that the transformation into vertex form is done correctly and that the signs are accurate when determining the vertex coordinates.
AI-generated content may contain errors. Please verify critical information