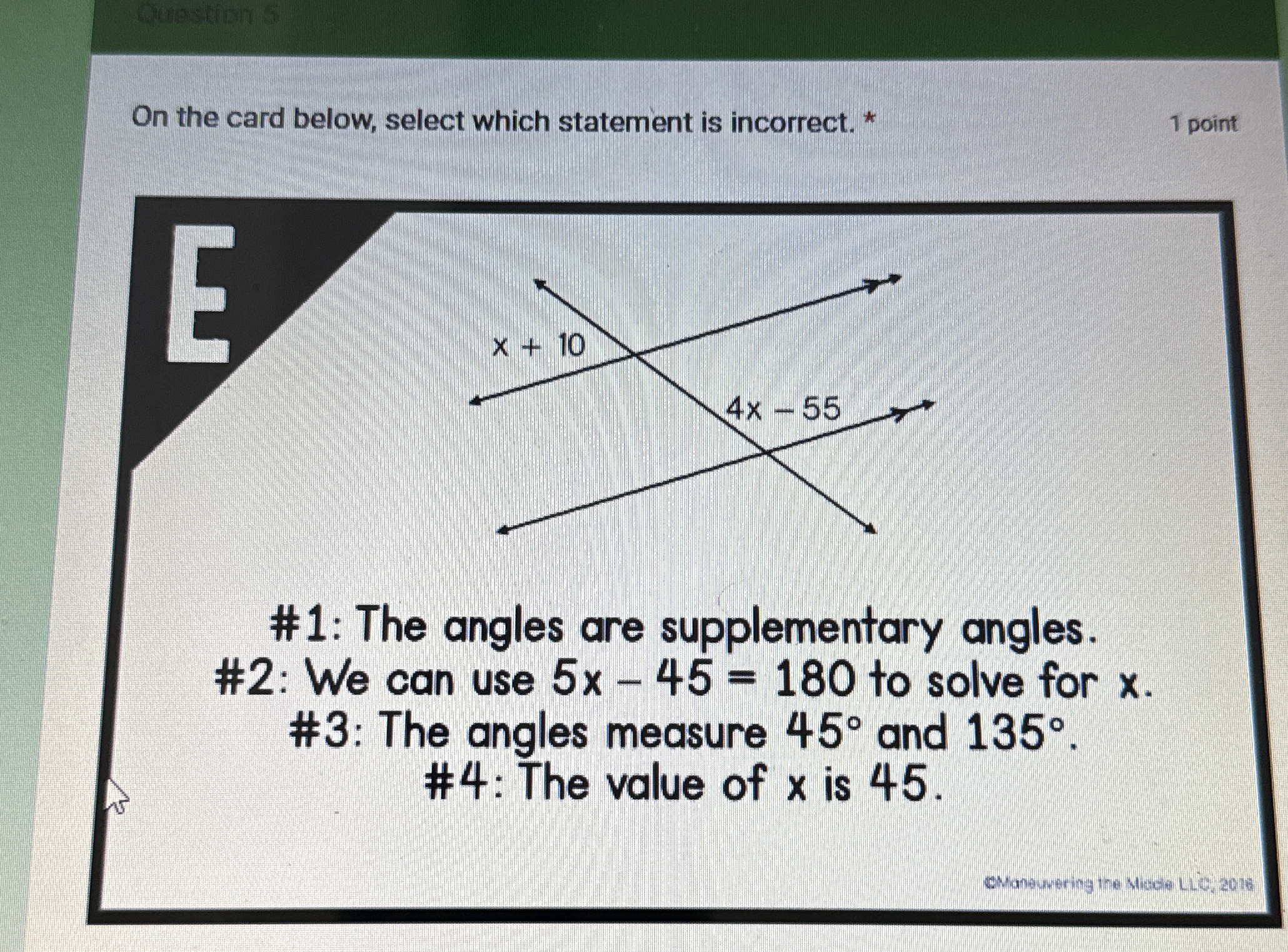
On the card below, select which statement is incorrect. #1: The angles are supplementary angles. #2: We can use 5x - 45 = 180 to solve for x. #3: The angles measure 45° and 135°. #... On the card below, select which statement is incorrect. #1: The angles are supplementary angles. #2: We can use 5x - 45 = 180 to solve for x. #3: The angles measure 45° and 135°. #4: The value of x is 45.
Understand the Problem
The question is asking which of the provided statements about the angles defined by the expressions x + 10 and 4x - 55 is incorrect. This involves understanding properties of angles, specifically supplementary angles and solving for variables.
Answer
Statement #3 is incorrect: The angles measure $55^\circ$ and $125^\circ$.
Answer for screen readers
Statement #3: "The angles measure $45^\circ$ and $135^\circ$" is incorrect.
Steps to Solve
-
Identify Angle Relationship The two angles defined by the expressions $x + 10$ and $4x - 55$ are formed by intersecting lines, making them supplementary angles. This means their measures add up to $180^\circ$.
-
Set Up the Equation To express this relationship mathematically, set up the equation: $$ (x + 10) + (4x - 55) = 180 $$
-
Simplify the Equation Combine like terms: $$ x + 10 + 4x - 55 = 180 $$ This simplifies to: $$ 5x - 45 = 180 $$
-
Solve for x Now isolate $x$: $$ 5x - 45 + 45 = 180 + 45 $$ $$ 5x = 225 $$ $$ x = \frac{225}{5} $$ $$ x = 45 $$
-
Evaluate Statements Now check each statement:
- Statement 1: The angles are supplementary angles. (True)
- Statement 2: We can use $5x - 45 = 180$ to solve for $x$. (True)
- Statement 3: The angles measure $45^\circ$ and $135^\circ$. (Evaluate this after finding $x$)
- Statement 4: The value of $x$ is $45$. (True; we found $x$)
- Check Measure of Each Angle Substituting $x = 45$ back into the angle expressions:
- First angle: $x + 10 = 45 + 10 = 55^\circ$
- Second angle: $4x - 55 = 4(45) - 55 = 180 - 55 = 125^\circ$ Thus the angles are $55^\circ$ and $125^\circ$, not $45^\circ$ and $135^\circ$.
Statement #3: "The angles measure $45^\circ$ and $135^\circ$" is incorrect.
More Information
The angles formed by the two lines in the diagram are not $45^\circ$ and $135^\circ$. Instead, we calculated them to be $55^\circ$ and $125^\circ$, confirming that statement #3 is false.
Tips
- Misinterpreting the angles formed by the intersecting lines as $45^\circ$ and $135^\circ$ without calculation.
- Not checking all statements thoroughly after solving.
AI-generated content may contain errors. Please verify critical information