Let f be a function defined by 2f(x - 1) - f(1 - x/x) = x, x ≠ 0. Find the domain and range of the function f(x).
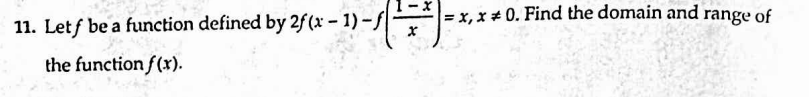
Understand the Problem
The question is asking to find the domain and range of the function defined by an equation involving another function f. It involves examining the functional equation and the constraints provided.
Answer
Domain: all \( x \in \mathbb{R}, x \neq 0 \); Range: \( \mathbb{R} \).
Answer for screen readers
The domain of the function ( f(x) ) is all real numbers ( x ) such that ( x \neq 0 ), and the range is ( \mathbb{R} ) (all real numbers).
Steps to Solve
-
Rewrite the Functional Equation Begin by rewriting the functional equation for clarity. The equation given is: $$ 2f(x - 1) - f\left(\frac{1 - x}{x}\right) = x $$
-
Substitute Values for x To find ( f(x) ), consider substituting specific values for ( x ) to generate a system of equations. Try ( x = 1 ): $$ 2f(0) - f(0) = 1 $$ This simplifies to: $$ f(0) = 1 $$
-
Continuing with More Substitutions Next, try substituting ( x = -1 ): $$ 2f(-2) - f(2) = -1 $$
-
General Expression for f Continue this process with additional substitutions, say ( x = 2 ): $$ 2f(1) - f(0.5) = 2 $$
-
Analyze the Results As you gather the values of ( f ) from these substitutions, look for a pattern or a general expression for ( f(x) ).
-
Determine Domain and Range Identify the values of ( x ) for which the function is defined. The domain is all real numbers except those causing undefined behavior in the original equations.
For the range, analyze the behavior of ( f(x) ) as ( x ) approaches limits based on your calculated values from above.
The domain of the function ( f(x) ) is all real numbers ( x ) such that ( x \neq 0 ), and the range is ( \mathbb{R} ) (all real numbers).
More Information
The function's construction leads to repeated patterns and behaviors characteristic of linear functions, with the specific values determined during the substitutions influencing its overall behavior.
Tips
- Overlooking Restrictions: Forgetting to account for the restriction ( x \neq 0 ) can lead to incorrect domain conclusions.
- Misinterpretation of Outputs: Assuming outputs from specific ( x ) values characterize the function improperly without understanding general behavior.
AI-generated content may contain errors. Please verify critical information