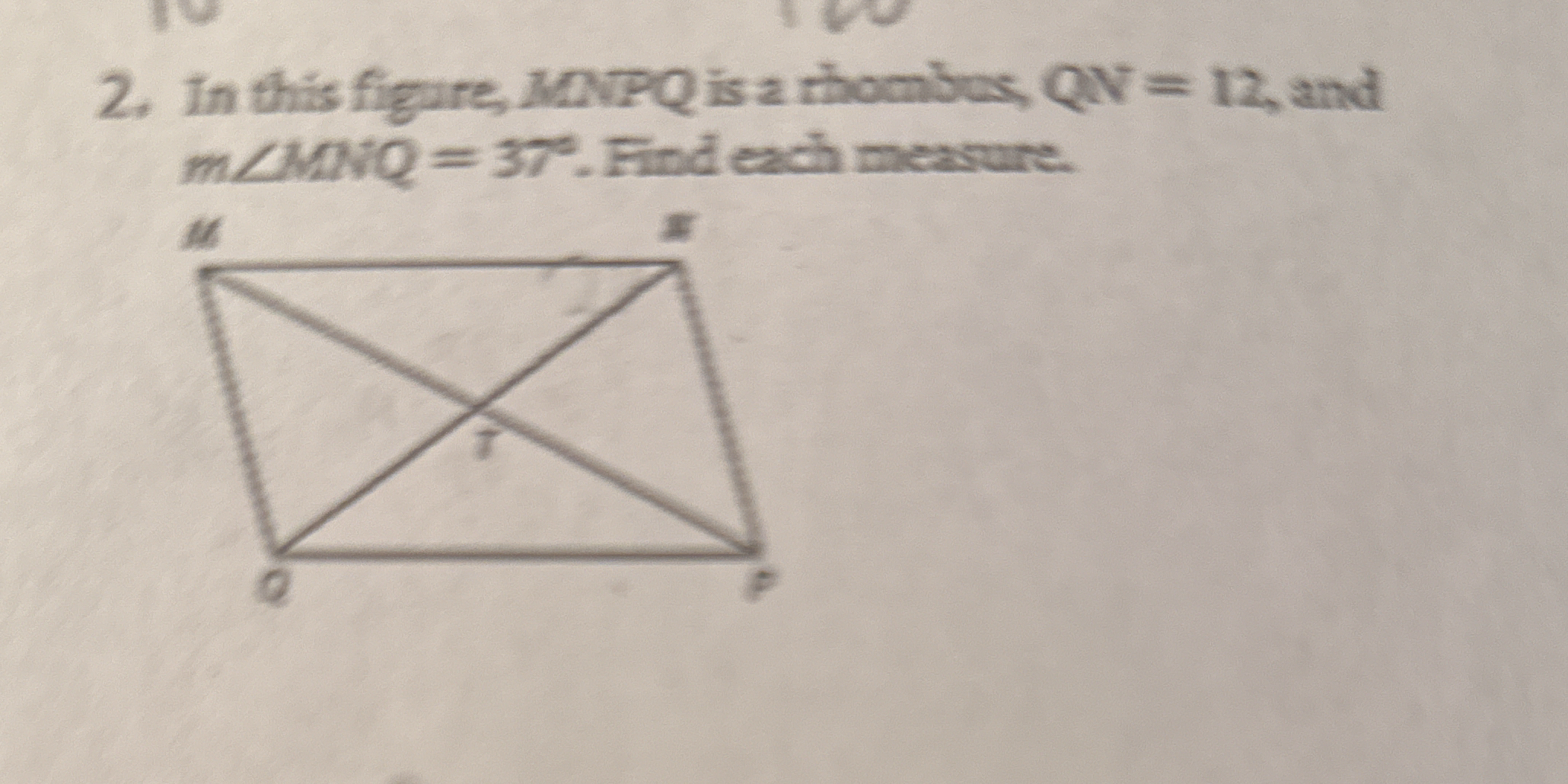
In this figure, MNQP is a rhombus, QN = 12, and m∠MNQ = 37°. Find each measure.

Steps to Solve

1. Understanding properties of a rhombus In a rhombus, all sides are of equal length and opposite angles are equal. The diagonals bisect each other at right angles.

2. Identifying the known values We know that the length of side $QN = 12$ and the measure of angle $m∠MNQ = 37°$. Since $MNQP$ is a rhombus, all sides $MN$, $QP$, and $MQ$ are also equal to $12$.

3. Finding the remaining angles Since opposite angles are equal in a rhombus, we have:

   • $m∠QPQ = 37°$ Therefore, the adjacent angles are supplementary: $$ m∠MQP + m∠MNQ = 180° $$ Thus, $$ m∠MQP = 180° - 37° = 143° $$

4. Finding the other angles Similarly, since the opposite angle to $m∠MQP$ is: $$ m∠PQM = 143° $$

5. Summary of angles The measures of the angles in the rhombus are:

   • $m∠MNQ = 37°$
   • $m∠QPQ = 37°$
   • $m∠MQP = 143°$
   • $m∠PQM = 143°$

6. Finding the lengths of diagonals Since the diagonals bisect at right angles, we can apply the Pythagorean theorem to find the diagonal lengths. Let's denote the diagonals as $d_1$ and $d_2$. Each diagonal can be calculated using: $$ \left(\frac{d_1}{2}\right)^2 + \left(\frac{d_2}{2}\right)^2 = 12^2 $$