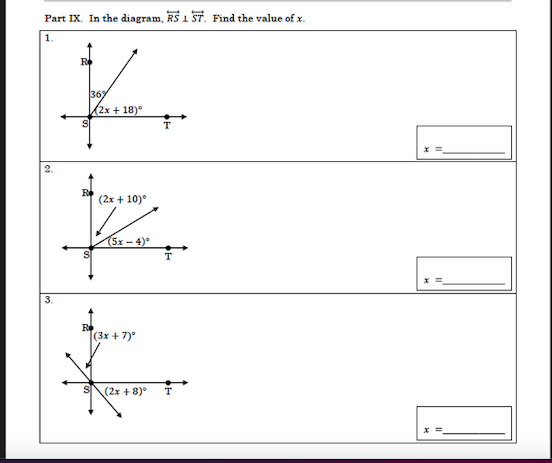
In the diagram, RS is parallel to ST. Find the value of x for the following angles: 1. 36° and (2x + 18)°, 2. (2x + 10)° and (5x - 4)°, 3. (3x + 7)° and (2x + 8)°.
Understand the Problem
The question provides a diagram with angles related to parallel lines and asks for the value of x in three separate cases. To solve it, we will apply the properties of angles formed by parallel lines and a transversal.
Answer
1. \( x = 9 \) 2. \( x = \frac{14}{3} \) 3. \( x = 1 \)
Answer for screen readers
-
( x = 9 )
-
( x = \frac{14}{3} ) (approximately ( 4.67 ))
-
( x = 1 )
Steps to Solve
-
Identify Angle Relationships for Each Case
For each problem, identify the corresponding angle relationships. When two parallel lines are crossed by a transversal, the alternate interior angles are equal, and corresponding angles are equal. -
Set Up Equations
Write equations based on the angle relationships for each case.- Case 1: Set (2x + 18 = 36) since they are corresponding angles.
- Case 2: Set (2x + 10 = 5x - 4) since they are supplementary angles.
- Case 3: Set (3x + 7 = 2x + 8) since they are alternate interior angles.
-
Solve for x in Each Case
Solve each equation for (x).-
Case 1:
$$ 2x + 18 = 36 $$
Subtract 18 from both sides:
$$ 2x = 18 $$
Divide by 2:
$$ x = 9 $$ -
Case 2:
$$ 2x + 10 = 5x - 4 $$
Rearranging gives:
$$ 10 + 4 = 5x - 2x $$
$$ 14 = 3x $$
Divide by 3:
$$ x = \frac{14}{3} \approx 4.67 $$ -
Case 3:
$$ 3x + 7 = 2x + 8 $$
Rearranging gives:
$$ 3x - 2x = 8 - 7 $$
$$ x = 1 $$
-
-
Write the Final Answers
Summarize the found values of (x) for each case.
-
( x = 9 )
-
( x = \frac{14}{3} ) (approximately ( 4.67 ))
-
( x = 1 )
More Information
The values of (x) were found by leveraging properties of angles formed with parallel lines and a transversal. Each scenario utilized either correspondence or the supplementary relationship of angles.
Tips
- Forgetting to correctly identify corresponding or alternate interior angles can lead to wrong equations.
- Misapplying the properties of angles, such as not accounting for supplementary angles, is common.
AI-generated content may contain errors. Please verify critical information