If x^2y^2 + 1/(x^2y^2) = 83, then the value of xy - 1/xy is?
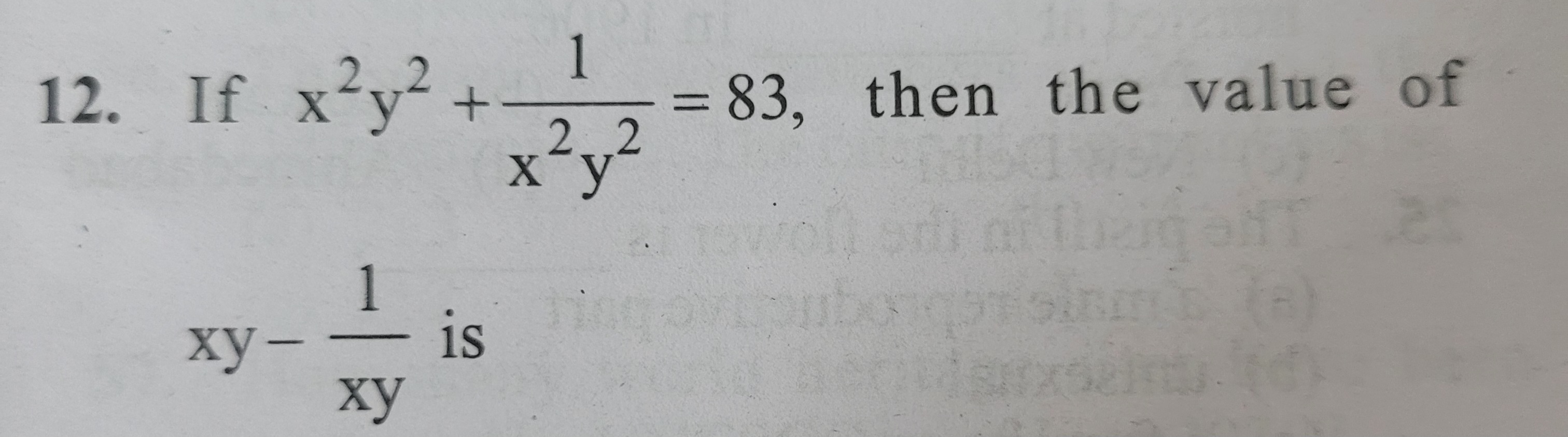
Understand the Problem
The question is asking to solve for the value of an expression given a specific equation involving variables x and y. It requires understanding of algebraic manipulation and possibly substitution or rearranging the formula.
Answer
The value of $xy - \frac{1}{xy}$ is $\sqrt{83 + \sqrt{6885}} - \frac{1}{\sqrt{83 + \sqrt{6885}}}$.
Answer for screen readers
The value of $xy - \frac{1}{xy}$ is $\sqrt{83 + \sqrt{6885}} - \frac{1}{\sqrt{83 + \sqrt{6885}}}$.
Steps to Solve
- Define a new variable for simplification
Let $z = xy$. Then, we can rewrite the given equation $x^2y^2 + \frac{1}{x^2y^2} = 83$ in terms of $z$: [ x^2y^2 = (xy)^2 = z^2 ] Thus, we can express the original equation as: [ z^2 + \frac{1}{z^2} = 83 ]
- Multiply through by (z^2)
To eliminate the fraction, multiply both sides of the equation by $z^2$: [ z^4 + 1 = 83z^2 ]
- Rearrange the equation to standard form
Rearranging gives: [ z^4 - 83z^2 + 1 = 0 ]
- Substitute (u = z^2)
Let (u = z^2). Then the equation becomes: [ u^2 - 83u + 1 = 0 ]
- Use the quadratic formula
Using the quadratic formula (u = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}), where (a = 1, b = -83, c = 1): [ u = \frac{83 \pm \sqrt{(-83)^2 - 4 \cdot 1 \cdot 1}}{2 \cdot 1} ] Calculating the discriminant: [ = \frac{83 \pm \sqrt{6889 - 4}}{2} = \frac{83 \pm \sqrt{6885}}{2} ]
- Find (z) from (u)
Since (u = z^2), we find: [ z = \sqrt{\frac{83 \pm \sqrt{6885}}{2}} ]
- Find the value of (xy - \frac{1}{xy})
We want to find the value of: [ xy - \frac{1}{xy} = z - \frac{1}{z} ] This can also be expressed as: [ = \frac{z^2 - 1}{z} ] Substituting (z^2 = u): [ = \frac{u - 1}{\sqrt{u}} ]
After calculating both possible values, we can find the respective values for $z$.
- Calculate (z - \frac{1}{z})
Using either value of (z): [ xy - \frac{1}{xy} = z - \frac{1}{z} = \sqrt{u} - \frac{1}{\sqrt{u}} ]
The value of $xy - \frac{1}{xy}$ is $\sqrt{83 + \sqrt{6885}} - \frac{1}{\sqrt{83 + \sqrt{6885}}}$.
More Information
This problem involves quadratic equations and manipulation of algebraic expressions, illustrating the use of variables and simplifications.
Tips
- Forgetting to multiply through by $z^2$ before rearranging.
- Misapplying the quadratic formula. Always verify calculations for $b^2 - 4ac$.
AI-generated content may contain errors. Please verify critical information