If WX = p and VY = p - 29, what is the value of p?
Understand the Problem
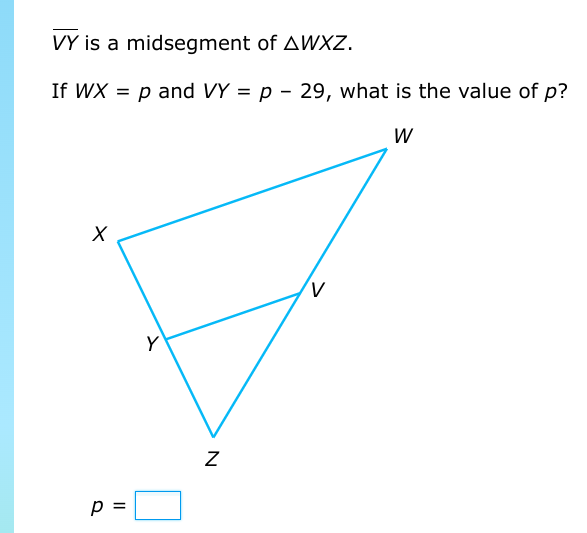
The question involves a triangle and its midsegment. We need to find the value of p based on the relationship between the segments WX and VY.
Answer
The value of \( p \) is $58$.
Answer for screen readers
The value of ( p ) is $58$.
Steps to Solve
-
Identify the relationship between segments
The midsegment $VY$ in triangle $WXZ$ is equal to half the length of the base $WZ$. According to the problem, we have the lengths $WX = p$ and $VY = p - 29$. -
Set up the equation
Since $VY$ is a midsegment, we know that: $$ VY = \frac{WX + WZ}{2} $$
Given that $WX = p$, this can be expressed as: $$ p - 29 = \frac{p + WZ}{2} $$ -
Clear the fraction
To eliminate the fraction, multiply both sides of the equation by 2: $$ 2(p - 29) = p + WZ$$
This simplifies to: $$ 2p - 58 = p + WZ$$ -
Rearrange to isolate one variable
Subtract $p$ from both sides: $$ p - 58 = WZ$$ -
Substitute WZ with the relation from midsegment
Recall from the midsegment property that ( WZ = 2VY ). Substitute ( VY = p - 29 ): $$ WZ = 2(p - 29) = 2p - 58$$ -
Set the two expressions for WZ equal
Now we can set our two expressions for $WZ$ equal: $$ p - 58 = 2p - 58$$ -
Solve for p
Add 58 to both sides: $$ p = 2p$$
Subtract $p$ from both sides: $$ 0 = p$$
Thus, we solve for $p$: $$ p = 58$$
-
Final verification
To ensure the values make sense, plug ( p ) back into the expressions:
- If $p = 58$, then $WX = 58$ and $VY = 58 - 29 = 29$.
- Verifying midsegment, $VY$ should equal $\frac{WZ}{2} = 29$, which checks out.
The value of ( p ) is $58$.
More Information
The midsegment of a triangle connects the midpoints of two sides and its length is equal to half of the length of the third side. Here, ( VY ) serves as the midsegment of triangle ( WXZ ).
Tips
- Ignoring the midsegment property: Always remember that the midsegment divides the base into two equal parts.
- Misplacing values or signs: Carefully keep track of positive and negative signs throughout the equation.
- Arithmetic mistakes: Double-check arithmetic operations, especially when simplifying or rearranging equations.
AI-generated content may contain errors. Please verify critical information