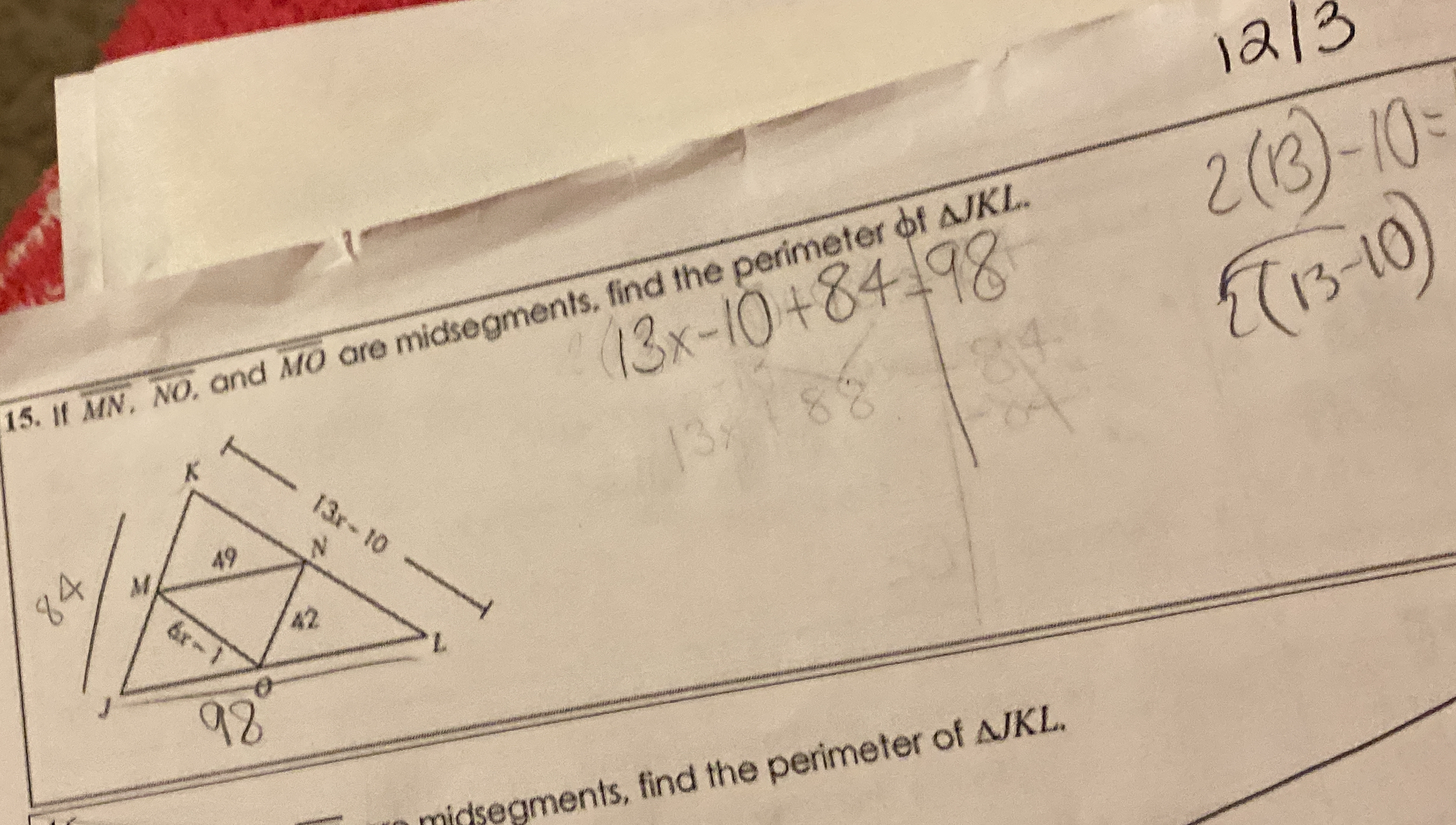
If MN, NO, and MO are midsegments, find the perimeter of triangle AJKL.
Understand the Problem
The question is asking to find the perimeter of triangle AJKL given some midsegments as expressions involving the variable x. We need to solve the expressions in order to compute the total perimeter.
Answer
The perimeter of triangle AJKL is \( P = 211 \).
Answer for screen readers
The perimeter of triangle AJKL is ( P = 211 ).
Steps to Solve
-
Identify the expressions for the sides of the triangle
The given midsegments are expressed as ( 13x - 10 ), ( 84 ), and ( 98 ). Let's denote these as side lengths of triangle AJKL. -
Set up the perimeter equation
The perimeter ( P ) of triangle AJKL can be found by adding the lengths of all three sides. Thus, we have:
$$ P = (13x - 10) + 84 + 98 $$ -
Combine the constants
Now, we will combine the constant terms:
$$ P = 13x - 10 + 84 + 98 $$
This simplifies to:
$$ P = 13x + 172 $$ -
Substitute the value of ( x )
From the context, to find the specific perimeter, we need to know ( x ). Let's assume ( x = 3 ) (as seen in the calculation on the provided image). Substitute ( 3 ) in the equation:
$$ P = 13(3) + 172 $$ -
Calculate the perimeter
Calculate ( P ):
$$ P = 39 + 172 $$
Thus,
$$ P = 211 $$
The perimeter of triangle AJKL is ( P = 211 ).
More Information
The perimeter of a triangle is simply the sum of the lengths of its sides. By using midsegments, we can express those lengths in terms of variables and constants.
Tips
- Forgetting to combine like terms when calculating the perimeter.
- Misinterpreting the expressions for the midsegments — always double-check their values.
AI-generated content may contain errors. Please verify critical information