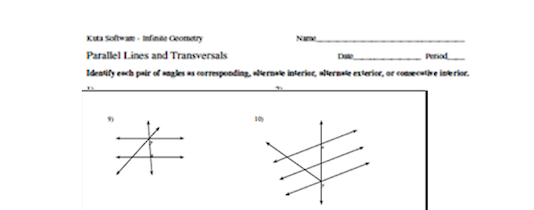
Identify each pair of angles as corresponding, alternate interior, alternate exterior, or consecutive interior.
Understand the Problem
The question is asking to identify pairs of angles formed by parallel lines and a transversal, categorizing them as corresponding, alternate interior, alternate exterior, or consecutive interior angles.
Answer
For both diagrams, the angles can be classified as corresponding, alternate interior, alternate exterior, or consecutive interior based on their positions related to the parallel lines and transversal.
Answer for screen readers
For each diagram:
Diagram 9:
- Corresponding Angles: (Angles 1 and 5, 2 and 6)
- Alternate Interior Angles: (Angles 3 and 5, 4 and 6)
- Alternate Exterior Angles: (Angles 1 and 4, 2 and 3)
- Consecutive Interior Angles: (Angles 3 and 6, 4 and 5)
Diagram 10:
- Corresponding Angles: (Angles 1 and 5, 2 and 6)
- Alternate Interior Angles: (Angles 3 and 5, 4 and 6)
- Alternate Exterior Angles: (Angles 1 and 4, 2 and 3)
- Consecutive Interior Angles: (Angles 3 and 6, 4 and 5)
Steps to Solve
-
Identify the Parallel Lines and Transversal
In each diagram, identify the two parallel lines and the transversal line that intersects them. Mark the intersection points to help visualize the angles formed. -
Label the Angles
Label the angles formed at each intersection. You can use numbers (1, 2, 3, etc.) or letters (A, B, C, etc.) to make it easier to reference each angle. -
Classify the Angles
Using the definitions of the angles:- Corresponding Angles: Angles that are on the same side of the transversal and in corresponding positions.
- Alternate Interior Angles: Angles that are on opposite sides of the transversal and inside the parallel lines.
- Alternate Exterior Angles: Angles that are on opposite sides of the transversal and outside the parallel lines.
- Consecutive Interior Angles: Angles that are on the same side of the transversal and inside the parallel lines.
-
Match Angle Pairs
For each set of labeled angles in the diagrams, determine which pairs match the definitions above and categorize them accordingly. -
State the Relationships Clearly
Write down the relationships for angle pairs clearly, indicating which angles are corresponding, alternate interior, alternate exterior, or consecutive interior.
For each diagram:
Diagram 9:
- Corresponding Angles: (Angles 1 and 5, 2 and 6)
- Alternate Interior Angles: (Angles 3 and 5, 4 and 6)
- Alternate Exterior Angles: (Angles 1 and 4, 2 and 3)
- Consecutive Interior Angles: (Angles 3 and 6, 4 and 5)
Diagram 10:
- Corresponding Angles: (Angles 1 and 5, 2 and 6)
- Alternate Interior Angles: (Angles 3 and 5, 4 and 6)
- Alternate Exterior Angles: (Angles 1 and 4, 2 and 3)
- Consecutive Interior Angles: (Angles 3 and 6, 4 and 5)
More Information
Understanding the relationships between angles formed by parallel lines and transversals is essential in geometry. These concepts are frequently applied in various fields such as engineering, architecture, and design, helping to calculate angles and create precise models.
Tips
- Confusing corresponding angles with alternate angles: Remember that corresponding angles are on the same side of the transversal.
- Overlooking the position of angles: Make sure you recognize whether angles are interior or exterior relative to the parallel lines.
- Neglecting to label angles: Labeling angles clearly can prevent mistakes in identification.
AI-generated content may contain errors. Please verify critical information