How many moles of aluminum oxide will be formed from 17 moles of aluminum reacting?
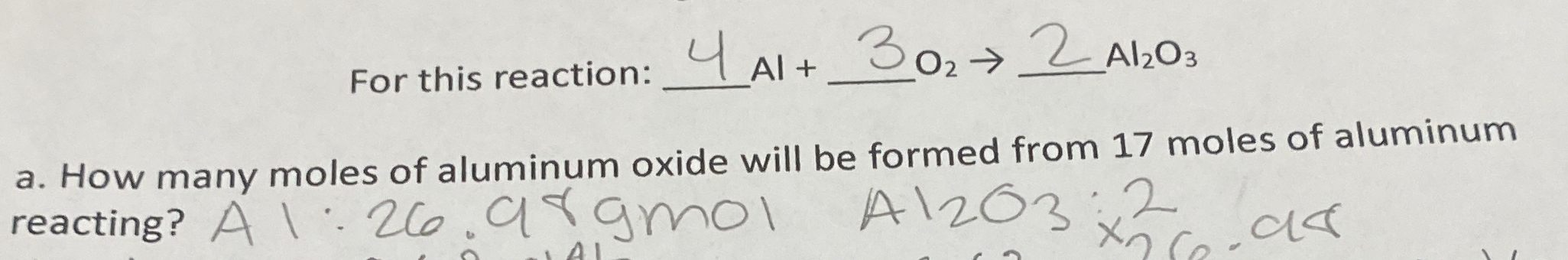
Understand the Problem
The question is asking how many moles of aluminum oxide (Al2O3) will be formed from the reaction of 17 moles of aluminum (Al), based on the stoichiometry of the provided chemical reaction. To determine this, we will use the mole ratio from the balanced equation.
Answer
The number of moles of aluminum oxide formed is $8.5$ moles.
Answer for screen readers
The number of moles of aluminum oxide (Al2O3) formed from 17 moles of aluminum (Al) is $8.5$ moles.
Steps to Solve
- Identify the mole ratio from the balanced equation
From the balanced chemical equation, we see that the stoichiometric ratio between aluminum (Al) and aluminum oxide (Al2O3) is given as: $$ 4 , \text{mol Al} \rightarrow 2 , \text{mol Al}_2\text{O}_3 $$
- Calculate the moles of Al2O3 formed
To find out how many moles of aluminum oxide will be formed from 17 moles of aluminum, we use the mole ratio: $$ \text{Moles of Al}_2\text{O}_3 = 17 , \text{moles Al} \times \frac{2 , \text{moles Al}_2\text{O}_3}{4 , \text{moles Al}} $$
- Perform the calculation
Now, we can simplify the calculation: $$ \text{Moles of Al}_2\text{O}_3 = 17 \times \frac{2}{4} = 17 \times 0.5 = 8.5 , \text{moles Al}_2\text{O}_3 $$
The number of moles of aluminum oxide (Al2O3) formed from 17 moles of aluminum (Al) is $8.5$ moles.
More Information
This calculation uses stoichiometry, which is essential for understanding reactants and products in chemical reactions. It ensures that mass is conserved in chemical processes.
Tips
- Misinterpreting the mole ratio. Ensure you match the correct coefficients from the balanced equation.
- Not simplifying the fraction properly. Always double-check your arithmetic to avoid errors.
AI-generated content may contain errors. Please verify critical information