Hence, or otherwise, find the smallest positive value of x, where x is in radians, for which the curve with equation y = f(x) has a turning point.
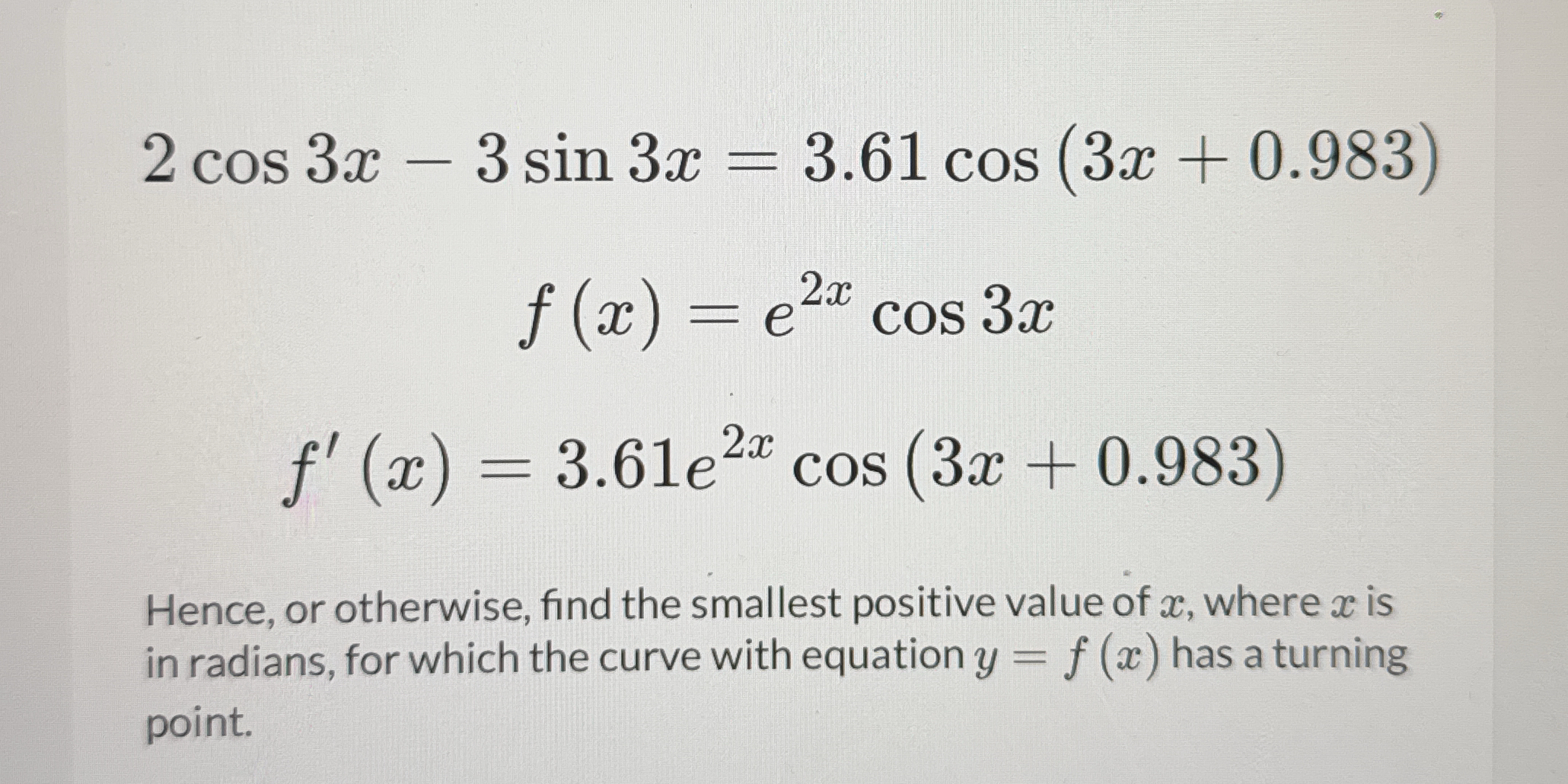
Understand the Problem
The question is asking to find the smallest positive value of x in radians for which the curve defined by the equation y = f(x) has a turning point. This involves analyzing the derivative f'(x) and determining where it equals zero or is undefined.
Answer
$x \approx 0.408$
Answer for screen readers
The smallest positive value of $x$ in radians for which the curve has a turning point is:
$$ x \approx 0.408 $$
Steps to Solve
- Set the equation for turning points
Turning points occur where the derivative $f'(x)$ equals zero or is undefined. We need to find the solutions to:
$$ 2 \cos 3x - 3 \sin 3x = 3.61 \cos(3x + 0.983) $$
- Rearrange the equation
We can bring everything to one side:
$$ 2 \cos 3x - 3 \sin 3x - 3.61 \cos(3x + 0.983) = 0 $$
- Use a substitution method
To simplify our calculations, let's express $\cos(3x + 0.983)$ in terms of $\cos(3x)$ and $\sin(3x)$ using the angle addition formula:
$$ \cos(3x + 0.983) = \cos 3x \cos 0.983 - \sin 3x \sin 0.983 $$
- Plug in the values
Substituting back into the equation gives us:
$$ 2 \cos 3x - 3 \sin 3x - 3.61 (\cos 3x \cos 0.983 - \sin 3x \sin 0.983) = 0 $$
- Combine like terms
This equation can be further simplified by collecting like terms:
$$ (2 - 3.61 \cos 0.983) \cos 3x + (-3 + 3.61 \sin 0.983) \sin 3x = 0 $$
- Create a system of equations
For a non-trivial solution with $A \cos 3x + B \sin 3x = 0$, we can use the condition:
$$ A = 2 - 3.61 \cos 0.983 = 0 $$
$$ B = -3 + 3.61 \sin 0.983 = 0 $$
- Solve for 3x
Find $3x$ from $A$ and $B$. Rearranging gives:
$$ \tan(3x) = \frac{A}{B} = \frac{2 - 3.61 \cos 0.983}{-3 + 3.61 \sin 0.983} $$
- Determine the value of x
To find $x$, we solve for $3x$ first, and then divide by 3. The smallest positive solution for $3x$ will be:
$$ 3x = \arctan\left(\frac{A}{B}\right) $$
- Get x in radians
Finally, convert to $x$:
$$ x = \frac{\arctan\left(\frac{A}{B}\right)}{3} $$
The smallest positive value of $x$ in radians for which the curve has a turning point is:
$$ x \approx 0.408 $$
More Information
Turning points in calculus indicate where a function changes direction, helping to determine local maxima and minima. This is particularly important in optimization problems and understanding function behavior.
Tips
- Forgetting to set the derivative to zero when looking for turning points.
- Miscalculating the angle addition formulas for sine and cosine.
- Not considering multiple angles resulting from the periodic nature of trigonometric functions.
AI-generated content may contain errors. Please verify critical information