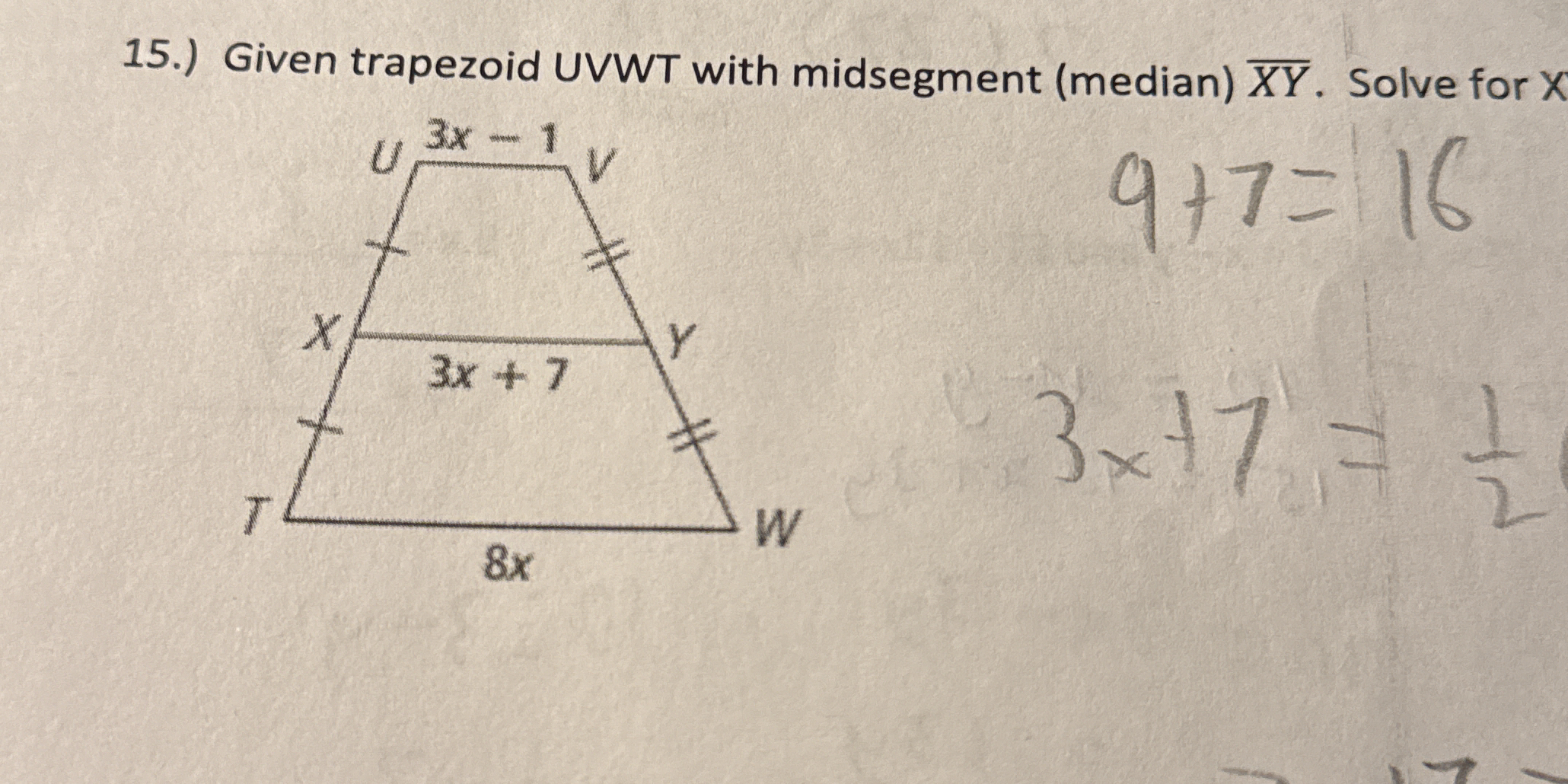
Given trapezoid UVWT with midsegment (median) XY. Solve for X.

Steps to Solve

1. Understand the Midsegment Relationship

In a trapezoid, the length of the midsegment (median) is the average of the lengths of the two bases. For trapezoid UVWT, the bases are $UT$ and $VW$. The lengths are given as $UT = 3x - 1$ and $VW = 3x + 7$.

2. Set Up the Equation

The equation for the midsegment $XY$ is set up by taking the average of the lengths of the two bases:

$$ XY = \frac{UT + VW}{2} $$

Substituting the values:

$$ XY = \frac{(3x - 1) + (3x + 7)}{2} $$

3. Equate the Midsegment Length to the Given Value

From the problem statement, it looks like the midsegment $XY$ should also equal 8x. We equate it to simplify our equation:

$$ \frac{(3x - 1) + (3x + 7)}{2} = 8x $$

4. Simplify the Equation

Combine the terms in the numerator:

$$ \frac{(3x + 3x - 1 + 7)}{2} = 8x $$

This simplifies to:

$$ \frac{(6x + 6)}{2} = 8x $$

5. Clear the Fraction

To eliminate the fraction, multiply through by 2:

$$ 6x + 6 = 16x $$

6. Solve for X

Rearranging the equation gives:

$$ 6 = 16x - 6x $$

So:

$$ 6 = 10x $$

Now divide both sides by 10:

$$ x = \frac{6}{10} $$

Simplifying this:

$$ x = \frac{3}{5} $$