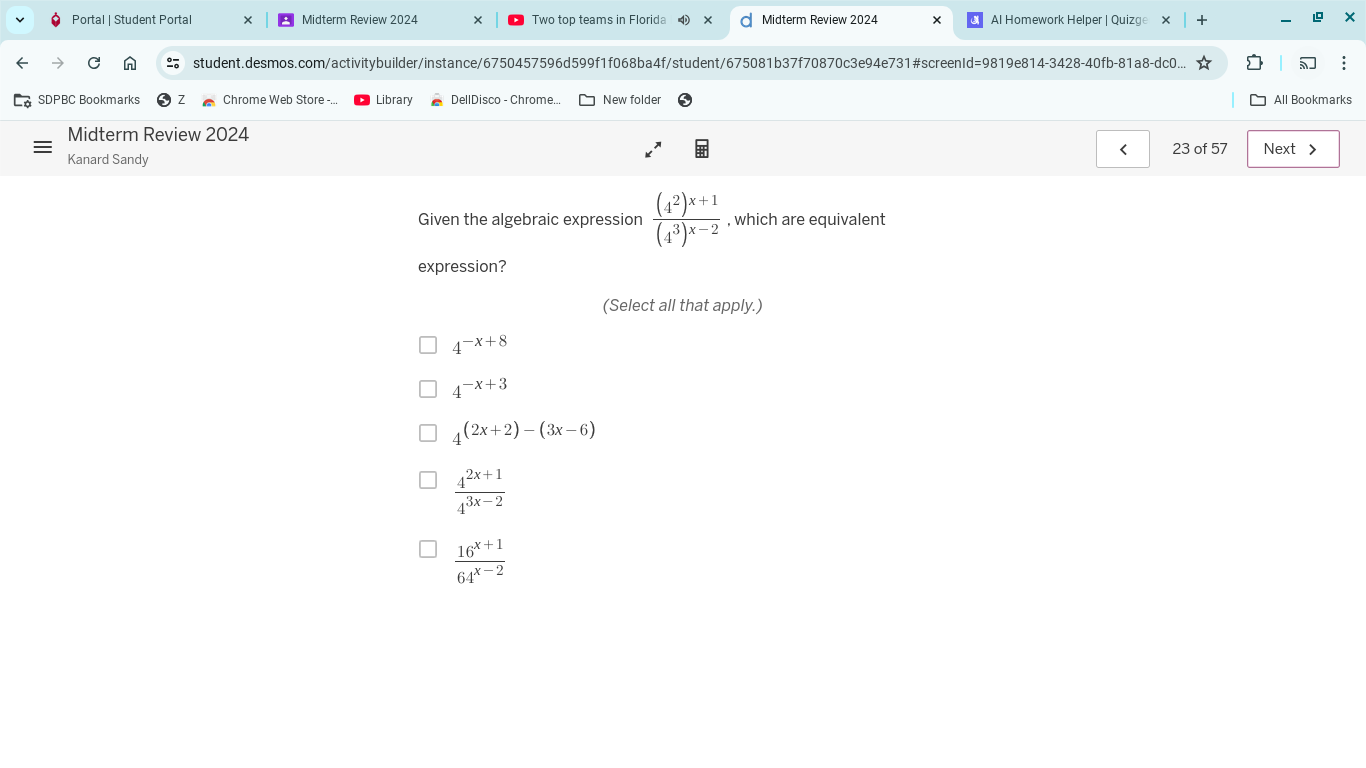
Given the algebraic expression (4^2)^(x+1) / (4^3)^(x-2), which are equivalent expressions? (Select all that apply.)

Understand the Problem

The question is asking for equivalent expressions to a given algebraic expression involving exponents and fractions. We need to identify which options from the provided list match the original expression when simplified or transformed appropriately.

Answer

The equivalent expressions are $ \frac{4^{2x + 1}}{3^{x - 2}} $ and $ \frac{16^{x + 1}}{64^{x - 2}} $.

Steps to Solve

Identify the given expression

The given expression is

$$ \left( \frac{4^2}{3^4} \right)^{x+1} $$

which simplifies to

$$ \frac{4^{2(x+1)}}{3^{4(x+1)}} $$

Expand the exponent

Expanding the exponent in the expression, we have:

$$ \frac{4^{2x + 2}}{3^{4x + 4}} $$

Expressing base 4 in terms of base 2

Since (4) can be written as (2^2), rewrite (4^{2x + 2}):

$$ 4^{2x + 2} = (2^2)^{2x + 2} = 2^{4x + 4} $$

Thus the expression becomes:

$$ \frac{2^{4x + 4}}{3^{4x + 4}} $$

Factor out common terms

We can factor this expression:

$$ \frac{2^{4x + 4}}{3^{4x + 4}} = \left( \frac{2}{3} \right)^{4x + 4} $$

Check equivalence with options

Now we need to compare this final expression with the given options to identify matching ones.

The equivalent expressions to the original expression are:

( 4^{2x + 1} / 3^{x - 2} )
( 16^{x + 1} / 64^{x - 2} )

More Information

The original expression simplifies to ( \left( \frac{2}{3} \right)^{4x + 4} ). Factoring out common terms can reveal equivalences more clearly. Recognizing base relationships like (4 = 2^2) is also useful in simplification.

Tips

Not knowing how to manipulate exponents properly.
Forgetting to change the bases when simplifying (e.g., not recognizing that (4 = 2^2)).
Overlooking the need to expand or reduce fractions involving exponents.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!