Fully simplify sqrt(54) + sqrt(24) / sqrt(2)
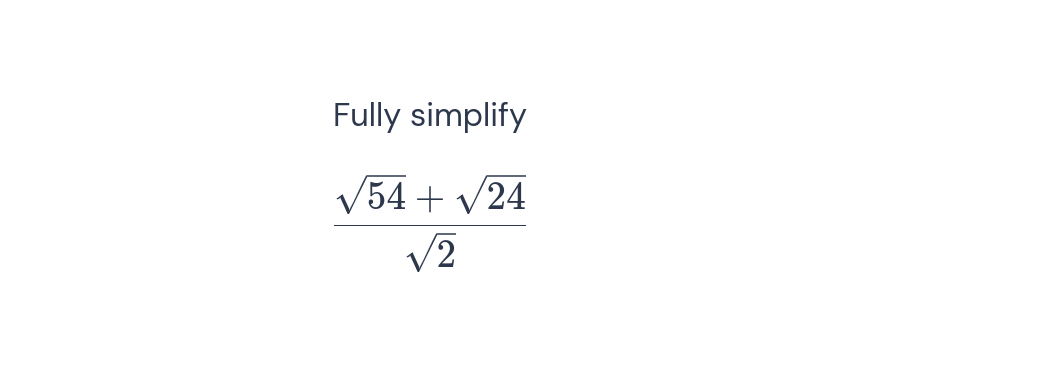
Understand the Problem
The question is asking to fully simplify the expression involving square roots. It includes finding the values of the square roots and simplifying the overall expression.
Answer
The fully simplified expression is \( 3\sqrt{6} + 2\sqrt{3} \).
Answer for screen readers
The fully simplified expression is ( 3\sqrt{6} + 2\sqrt{3} ).
Steps to Solve
-
Simplify ( \sqrt{54} ) First, factor ( 54 ) into its prime factors: $$ 54 = 9 \times 6 = 3^2 \times 6 $$ Now, simplify the square root: $$ \sqrt{54} = \sqrt{9 \times 6} = \sqrt{9} \times \sqrt{6} = 3\sqrt{6} $$
-
Simplify ( \sqrt{24} ) Next, factor ( 24 ): $$ 24 = 4 \times 6 = 2^2 \times 6 $$ Now, simplify the square root: $$ \sqrt{24} = \sqrt{4 \times 6} = \sqrt{4} \times \sqrt{6} = 2\sqrt{6} $$
-
Divide ( \sqrt{24} ) by ( \sqrt{2} ) Now, simplify the division: $$ \sqrt{24} \div \sqrt{2} = \frac{\sqrt{24}}{\sqrt{2}} = \sqrt{\frac{24}{2}} = \sqrt{12} $$ Next, simplify ( \sqrt{12} ): $$ \sqrt{12} = \sqrt{4 \times 3} = \sqrt{4} \times \sqrt{3} = 2\sqrt{3} $$
-
Combine the expressions Now, combine ( 3\sqrt{6} ) and ( 2\sqrt{3} ): $$ 3\sqrt{6} + 2\sqrt{3} $$
This expression is simplified and cannot be combined further since ( \sqrt{6} ) and ( \sqrt{3} ) are not like terms.
The fully simplified expression is ( 3\sqrt{6} + 2\sqrt{3} ).
More Information
In simplifying square roots, it's essential to factor out perfect squares to simplify the square root expression correctly. This process demonstrates the importance of identifying and breaking down numbers into their prime factors.
Tips
- Ignoring simplifications: One common mistake is not simplifying square roots completely. Always check to see if you can factor out perfect squares.
- Mistaking operations: Be careful not to misapply division rules with square roots, as this can lead to errors in simplification. Always simplify the fraction before taking the square root.
AI-generated content may contain errors. Please verify critical information