∑ (from k=1 to n) (-1)^(k+1) 2k
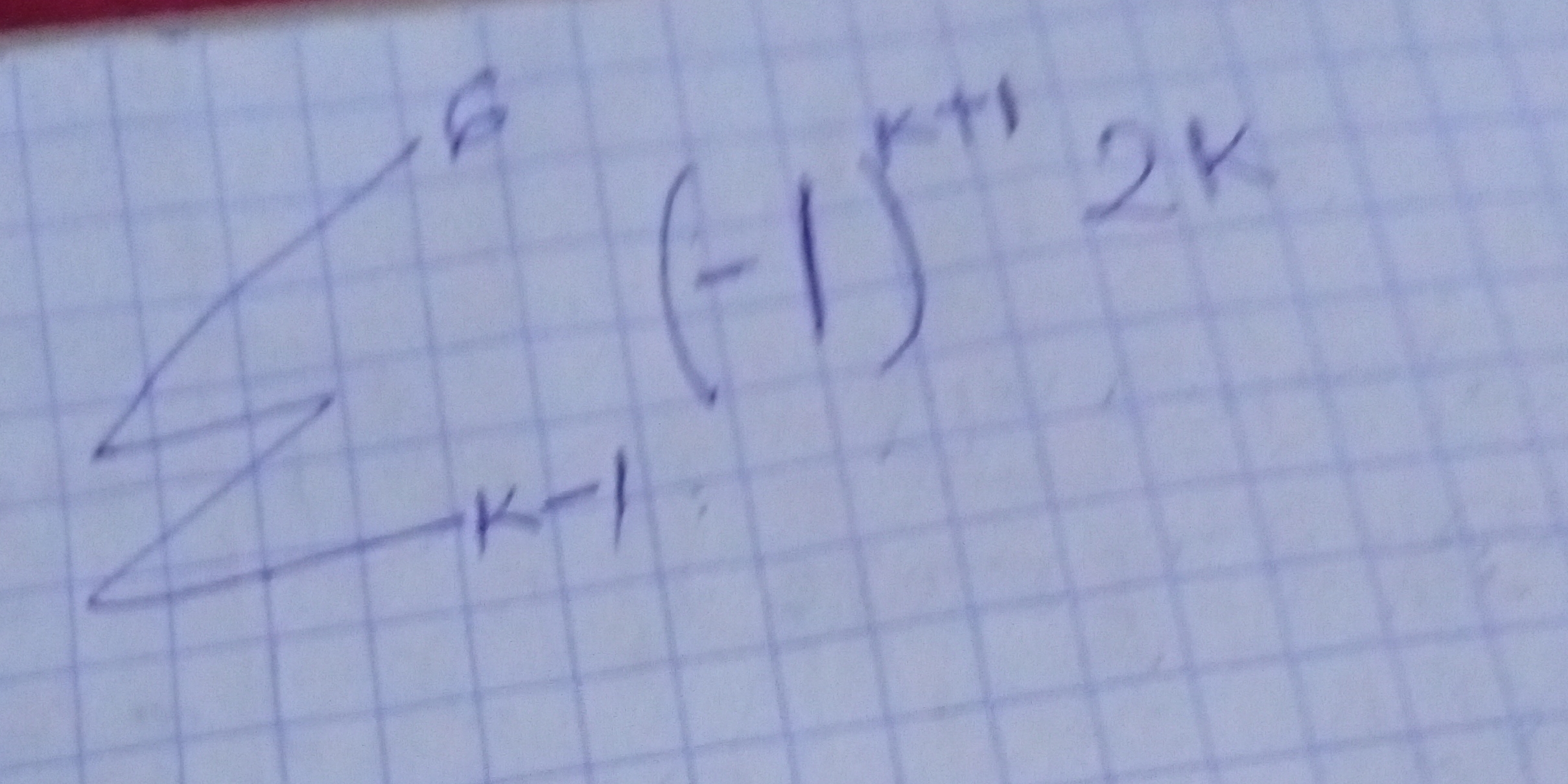
Understand the Problem
The question involves a mathematical equation, likely requiring the application of summation notation and some algebraic manipulation. It appears to relate to a series where 'k' is a variable.
Answer
For $n$ even: $S = -n$; for $n$ odd: $S = n + 2$.
Answer for screen readers
The result of the summation is:
- If $n$ is even, $S = -n$.
- If $n$ is odd, $S = n + 2$.
Steps to Solve
- Understanding the Summation Notation
The expression given is a summation: $$ \sum_{k=1}^{n} (-1)^{k+1} 2k $$ This means we will sum the terms generated by the formula $(-1)^{k+1} 2k$ for each integer value of $k$ starting from 1 and going up to $n$.
- Evaluating the Terms of the Sum
Let's calculate a few terms to observe the pattern:
- For $k=1$: $(-1)^{1+1} 2(1) = 2$
- For $k=2$: $(-1)^{2+1} 2(2) = -4$
- For $k=3$: $(-1)^{3+1} 2(3) = 6$
- For $k=4$: $(-1)^{4+1} 2(4) = -8$
The series alternates between adding and subtracting values.
- Formulating the Series
The series can be expressed as: $$ S = 2 - 4 + 6 - 8 + ... + (-1)^{n+1} 2n $$ We separate it into the sum of even and odd indexed elements.
- Finding the General Formula
When $n$ is odd:
- Positive terms: $2 + 6 + ... + 2n = 2(1 + 3 + \ldots + n) \Rightarrow$ (Sum of first n odd numbers = $n^2$)
- Negative terms: $-4 - 8 - ... - 2(n-1) = -2(2 + 4 + ... + (n-1)) \Rightarrow$ (Arithmetic series sum)
When $n$ is even:
- Positive terms and negative terms can be summed similarly.
- Expressing The Final Result
To find the final sum, we can derive that: For even $n$: $$ S_n = -n $$
For odd $n$: $$ S_n = n + 2 $$
The result of the summation is:
- If $n$ is even, $S = -n$.
- If $n$ is odd, $S = n + 2$.
More Information
This summation represents an alternating series where the positive contributions increase while negative contributions grow larger in magnitude with each iteration. Such series are common in various mathematical applications, including calculus and number theory.
Tips
- Not properly alternately summing the terms correctly could lead to errors.
- Forgetting to handle even and odd cases separately can cause incorrect results.
AI-generated content may contain errors. Please verify critical information