Find the solution to the system of equations g(x) = -3x + 5.
Understand the Problem
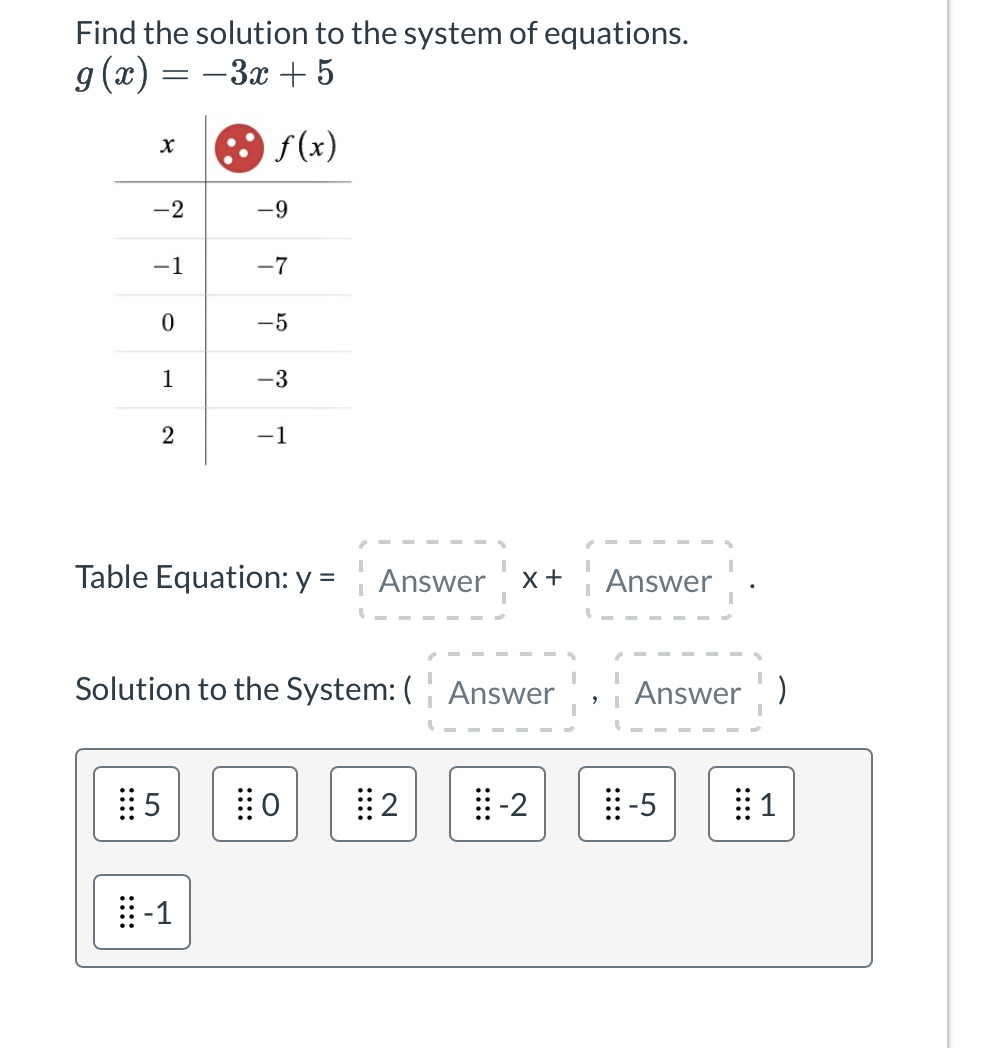
The question is asking for the solution to a system of equations that includes a linear function g(x) = -3x + 5 and data from a table that shows values of f(x) for corresponding x values. The user needs to find the equation of the line represented by the table and the solution point where the two functions intersect.
Answer
Table Equation: \( y = 2x - 5 \) Solution to the System: \( (2, -1) \)
Answer for screen readers
The table equation is ( y = 2x - 5 ).
The solution to the system is ( (2, -1) ).
Steps to Solve
- Identify the Points from the Table
From the given table, we extract the values of ( f(x) ) for the corresponding ( x ) values:
- At ( x = -2, f(-2) = -9 )
- At ( x = -1, f(-1) = -7 )
- At ( x = 0, f(0) = -5 )
- At ( x = 1, f(1) = -3 )
- At ( x = 2, f(2) = -1 )
- Determine the Slope of the Line ( f(x) )
To find the slope ( m ) of the line represented by the points, we can choose two points, for example, ( (-2, -9) ) and ( (2, -1) ).
Using the slope formula:
$$ m = \frac{y_2 - y_1}{x_2 - x_1} $$
Substituting:
$$ m = \frac{-1 - (-9)}{2 - (-2)} = \frac{-1 + 9}{2 + 2} = \frac{8}{4} = 2 $$
- Formulate the Equation of Line ( f(x) )
Now, we can use the slope-intercept formula ( y = mx + b ). We know ( m = 2 ). To find ( b ), we can use one of the points, say ( (0, -5) ):
$$ -5 = 2(0) + b $$
This gives us ( b = -5 ).
Thus, the equation of the line is:
$$ f(x) = 2x - 5 $$
- Set the Equations Equal to Find the Intersection
Now, set ( g(x) ) equal to ( f(x) ):
$$ -3x + 5 = 2x - 5 $$
- Solve for ( x )
Combine like terms:
$$ 5 + 5 = 2x + 3x $$
This simplifies to:
$$ 10 = 5x $$
Now solve for ( x ):
$$ x = \frac{10}{5} = 2 $$
- Find the Corresponding ( y ) Value
Substituting ( x = 2 ) into either function to find ( y ):
Using ( g(x) ):
$$ g(2) = -3(2) + 5 = -6 + 5 = -1 $$
- Write the Solution Point
The point where the two functions intersect is:
$$ (2, -1) $$
The table equation is ( y = 2x - 5 ).
The solution to the system is ( (2, -1) ).
More Information
The point ( (2, -1) ) indicates the ( x ) and ( y ) values where the two linear equations intersect, meaning both functions have the same value at this point.
Tips
- Miscalculating the slope: Always ensure to choose correct points and apply the slope formula accurately.
- Forgetting to check the result in both equations: It's good practice to substitute the ( x ) value back into both functions to verify correctness.
AI-generated content may contain errors. Please verify critical information