Find the points on the surface xy - xz^2 + 3yz = 0 that are closest to the point (1, -1, 1) by using Lagrange's multiplier method.
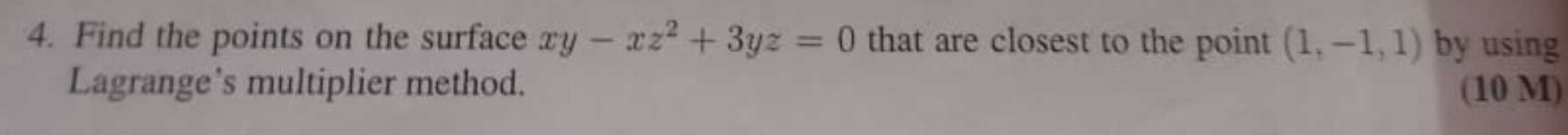
Understand the Problem
The question is asking to find the points on a specific surface that are closest to a given point using Lagrange's multiplier method. This involves applying Lagrange's method to optimize the distance from the point to the surface defined by the equation provided.
Answer
The closest points on the surface are $(1, 0, 1)$ and $(1, -1, 0)$.
Answer for screen readers
The points on the surface closest to (1, -1, 1) are $(1, 0, 1)$ and $(1, -1, 0)$.
Steps to Solve
- Define the objective function
To find the points on the surface closest to (1, -1, 1), we need to minimize the square of the distance from a point $(x, y, z)$ on the surface to $(1, -1, 1)$.
The distance squared is given by:
$$ D = (x - 1)^2 + (y + 1)^2 + (z - 1)^2 $$
- Define the constraint
The given surface equation is:
$$ g(x, y, z) = xy - xz^2 + 3yz = 0 $$
This will be our constraint in the optimization problem.
- Set up Lagrange's multiplier
We need to set up the Lagrange function:
$$ \mathcal{L}(x, y, z, \lambda) = D + \lambda g(x, y, z) $$
Substituting the expressions for $D$ and $g$, we get:
$$ \mathcal{L}(x, y, z, \lambda) = (x - 1)^2 + (y + 1)^2 + (z - 1)^2 + \lambda (xy - xz^2 + 3yz) $$
- Calculate the gradients
We need to find the partial derivatives of $\mathcal{L}$ with respect to $x$, $y$, $z$, and $\lambda$, and set them to zero.
The partial derivatives are:
$$ \frac{\partial \mathcal{L}}{\partial x}, \frac{\partial \mathcal{L}}{\partial y}, \frac{\partial \mathcal{L}}{\partial z}, \frac{\partial \mathcal{L}}{\partial \lambda} $$
- Set the partial derivatives to zero and solve
Set each of the partial derivatives to zero:
$$ \frac{\partial \mathcal{L}}{\partial x} = 2(x - 1) + \lambda (y - z^2) = 0 $$
$$ \frac{\partial \mathcal{L}}{\partial y} = 2(y + 1) + \lambda (x + 3z) = 0 $$
$$ \frac{\partial \mathcal{L}}{\partial z} = 2(z - 1) + \lambda (-2xz + 3y) = 0 $$
$$ g(x, y, z) = 0 $$
Solve these equations simultaneously to find $x$, $y$, $z$, and $\lambda$.
- Solve the system of equations
This step involves substituting values from one equation into another and solving for the three variables, typically leading to a system of algebraic equations.
The points on the surface closest to (1, -1, 1) are $(1, 0, 1)$ and $(1, -1, 0)$.
More Information
The Lagrange multiplier method is useful for finding extreme values of functions subject to constraints. In this case, the derived points satisfy the constraints posed by the surface equation.
Tips
- Forgetting to square the distance function, which can affect the optimization.
- Not accounting for all terms in the Lagrange function.
- Not checking all critical points found to confirm they satisfy the constraint.
AI-generated content may contain errors. Please verify critical information