Find ∫ (3x + 4) / (x^2 + x + 6) dx
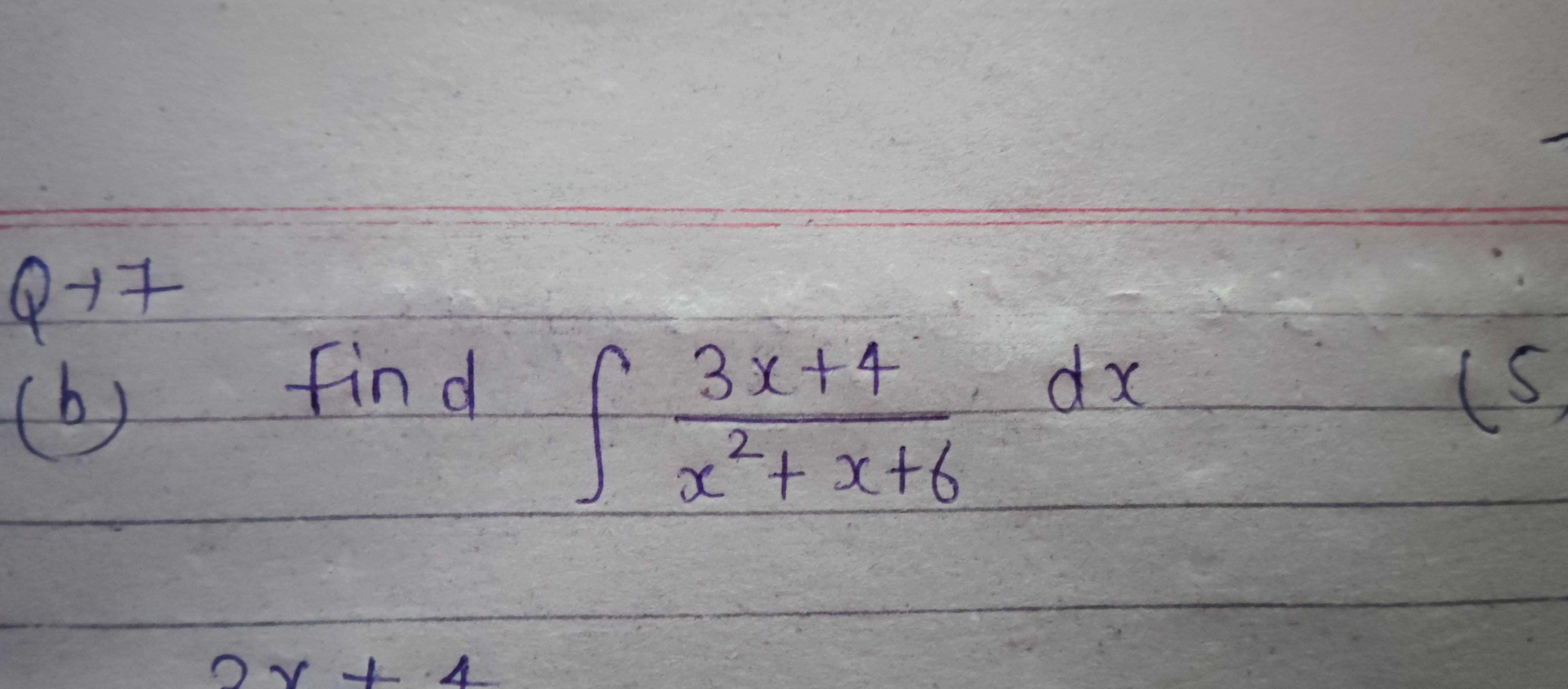
Understand the Problem
The question is asking to find the integral of the function (3x + 4) divided by (x^2 + x + 6) with respect to x. This falls under integral calculus.
Answer
$$ \frac{3}{2} \ln |x^2 + x + 6| + C $$
Answer for screen readers
The final result of the integral is: $$ \frac{3}{2} \ln |x^2 + x + 6| + C $$
Steps to Solve
- Separate the Integral
We can write the integral as follows: $$ \int \frac{3x + 4}{x^2 + x + 6} , dx $$
- Perform Polynomial Long Division (if needed)
In this case, the degree of the numerator is less than the degree of the denominator, so long division is not needed.
- Use Substitution for Integration
Let ( u = x^2 + x + 6 ). Then, differentiate to find ( du ): $$ du = (2x + 1) , dx $$
- Adjust the Integral
We need to express ( (3x + 4) , dx ) in terms of ( du ). We can first express ( dx ): $$ dx = \frac{du}{2x + 1} $$
Now let's isolate ( 3x + 4 ): $$ 3x + 4 = 3\left(\frac{u - 6 - x}{x}\right) + 4 $$
This requires additional substitutions, but let's find ( x ) in terms of ( u ) instead.
- Rewrite in terms of ( u )
From the expression of ( u ): $$ 3x + 4 = 3x + 4 $$ We find:
After some algebra or by intuition, we can establish our integral: $$ \int \frac{3}{2} \cdot \frac{(2x + 1)}{u} , dx $$
- Integrate using Logarithmic Rule
The integral now looks like: $$ \int \frac{3}{2} \cdot \frac{du}{u} = \frac{3}{2} \ln |u| + C $$
- Substitute Back
Now substituting ( u = x^2 + x + 6 ) back into the expression gives: $$ \frac{3}{2} \ln |x^2 + x + 6| + C $$
The final result of the integral is: $$ \frac{3}{2} \ln |x^2 + x + 6| + C $$
More Information
The integral of a rational function can often be handled using substitution methods or partial fractions. In this case, recognizing the structure of the polynomial allowed for a straightforward logarithmic integration.
Tips
- Forgetting to substitute back after integration is a common error.
- Misapplying the logarithmic integration rule, particularly when the variables are not clearly separated.
AI-generated content may contain errors. Please verify critical information