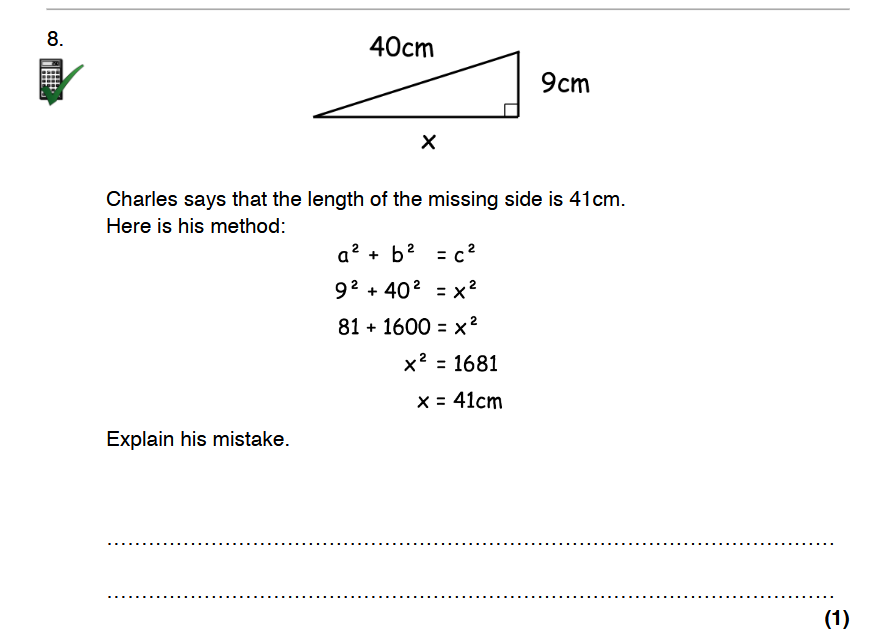
Explain Charles's mistake in his calculation of the missing side of the triangle.

Understand the Problem

The question asks us to identify and explain Charles's mistake in his calculation using the Pythagorean theorem for a right triangle. We need to analyze his steps and find where he went wrong, particularly in the application of the theorem and the resultant arithmetic.

Answer

The length of the missing side $x$ is approximately $38.99$ cm.

Steps to Solve

Identify the correct application of the Pythagorean theorem

The Pythagorean theorem states that in a right triangle:

$$ a^2 + b^2 = c^2 $$

Where $a$ and $b$ are the lengths of the two legs, and $c$ is the length of the hypotenuse.

In this case, $a = 9$ cm and $c = 40$ cm.

Set up the correct equation

Charles incorrectly sets $b$ as $40$ cm. However, $40$ cm is actually the hypotenuse, not a leg. The correct equation should be:

$$ 9^2 + x^2 = 40^2 $$

Calculate the squares

Now calculate the squares:

For the leg:

$$ 9^2 = 81 $$

For the hypotenuse:

$$ 40^2 = 1600 $$

Set up the new equation

The equation should now look like this:

$$ 81 + x^2 = 1600 $$

Solve for $x^2$

To find $x^2$, first subtract $81$ from both sides:

$$ x^2 = 1600 - 81 $$

Calculating:

$$ 1600 - 81 = 1519 $$

Therefore,

$$ x^2 = 1519 $$

Find the value of $x$

Take the square root of both sides:

$$ x = \sqrt{1519} $$

Calculating this gives:

$$ x \approx 38.99 cm $$

The correct length of the missing side $x$ is approximately $38.99$ cm.

More Information

Charles mistakenly used the length of the hypotenuse as one of the legs in his calculation. By incorrectly applying the sides of the triangle in the Pythagorean theorem, he arrived at an incorrect value for $x$.

Tips

Misidentifying the sides of the triangle; ensure you know which sides are legs and which is the hypotenuse.
Incorrectly calculating the squares or making arithmetic errors.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!