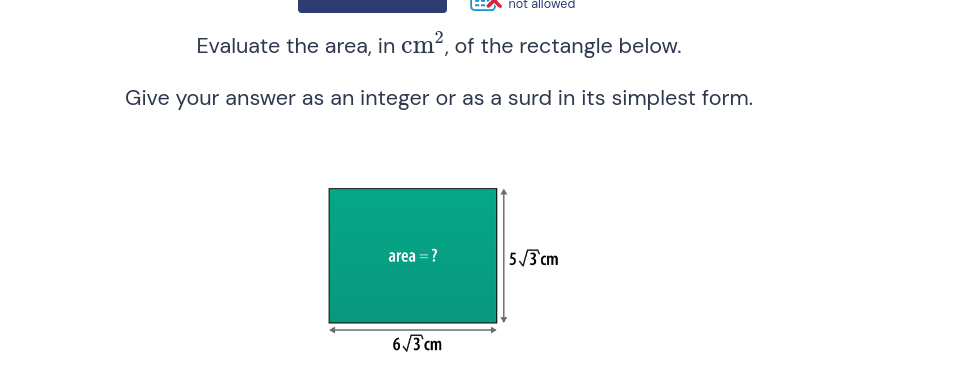
Evaluate the area, in cm², of the rectangle below. Give your answer as an integer or as a surd in its simplest form.
Understand the Problem
The question is asking to calculate the area of a rectangle with given dimensions in surd form. The area can be determined by multiplying the length and width of the rectangle.
Answer
The area of the rectangle is $90 \, \text{cm}^2$.
Answer for screen readers
The area of the rectangle is $90 , \text{cm}^2$.
Steps to Solve
- Identify the dimensions of the rectangle
The rectangle has a length of $6\sqrt{3} , \text{cm}$ and a width of $5\sqrt{3} , \text{cm}$.
- Calculate the area formula
The area $A$ of a rectangle can be calculated using the formula:
$$ A = \text{length} \times \text{width} $$
- Substitute the dimensions into the formula
Using the identified dimensions:
$$ A = (6\sqrt{3}) \times (5\sqrt{3}) $$
- Calculate the product
Multiply the coefficients and the surds separately:
- Coefficients: $6 \times 5 = 30$
- Surds: $\sqrt{3} \times \sqrt{3} = 3$
Combine these results:
$$ A = 30 \times 3 = 90 , \text{cm}^2 $$
The area of the rectangle is $90 , \text{cm}^2$.
More Information
The area of a rectangle is straightforward to calculate when you know its dimensions. Surds are often used in mathematics to express irrational numbers, and calculating with them requires careful multiplication.
Tips
- Ignoring the surd multiplication: Sometimes, one may forget to multiply the surds correctly.
- Not simplifying the final answer: Ensure to combine the coefficients and surds properly for the final area.
AI-generated content may contain errors. Please verify critical information