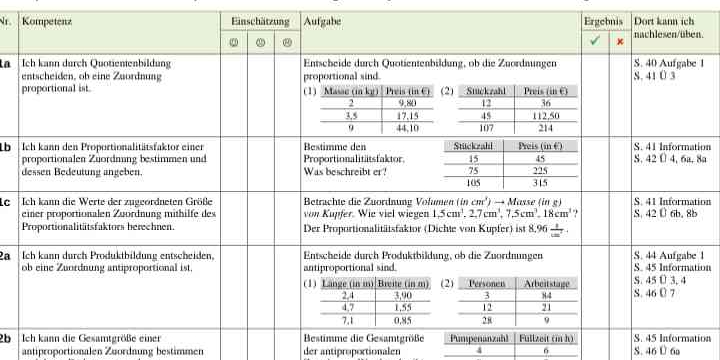
Entscheide durch Quotientenbildung, ob die Zuordnungen proportional sind.
Understand the Problem
Die Frage bezieht sich auf verschiedene mathematische Aufgaben und Konzepte, insbesondere auf proportionale und antiproportionale Zuordnungen sowie die Berechnung von Proportionalitätsfaktoren. Es scheint, dass die Aufgaben in einer Tabelle zur Selbstbewertung oder Übung präsentiert werden.
Answer
Proportionale Zuordnungen, $k = \frac{Masse}{Preis}$.
Answer for screen readers
Die Zuordnungen sind proportional, wenn die Quotienten der jeweiligen Werte gleich sind. Der Proportionalitätsfaktor ist: $$ k = \frac{Masse}{Preis} $$
Steps to Solve
-
Analyse der gegebenen Daten Identifiziere die Beziehungen zwischen den verschiedenen Größen in der Tabelle. Zum Beispiel, wenn die Beziehung zwischen Masse und Preis untersucht wird.
-
Berechnung von Quotienten Berechne die Quotienten, um zu sehen, ob eine proportionale Beziehung besteht. Zum Beispiel für die Masse und den Preis: Berechne den Quotienten für verschiedene Paare:
- Erster Quotient: $\frac{2.5}{9.40}$
- Zweiter Quotient: $\frac{3.5}{12.50}$
-
Vergleich der Quotienten Vergleiche die berechneten Quotienten. Wenn sie gleich sind, ist die Zuordnung proportional.
-
Bestimmung des Proportionalitätsfaktors Wenn die Zuordnung proportional ist, bestimme den Proportionalitätsfaktor (k): $$ k = \frac{Masse}{Preis} $$
-
Prüfung anderer Zuordnungen Führe eine ähnliche Vorgehensweise für die anderen Zuordnungen in der Tabelle durch, um festzustellen, ob sie proportional oder antiproportional sind.
Die Zuordnungen sind proportional, wenn die Quotienten der jeweiligen Werte gleich sind. Der Proportionalitätsfaktor ist: $$ k = \frac{Masse}{Preis} $$
More Information
Proportionalität bedeutet, dass zwei Größen immer im gleichen Verhältnis zueinander stehen. Dies wird oft in Alltagskontexten wie bei der Preisgestaltung oder bei der Berechnung von Dichten verwendet.
Tips
- Den Quotienten nicht korrekt berechnen.
- Übersehen, dass Proportionalität nur gegeben ist, wenn alle Quotienten identisch sind.
- Verwechseln von proportionalen und antiproportionalen Zuordnungen.
AI-generated content may contain errors. Please verify critical information