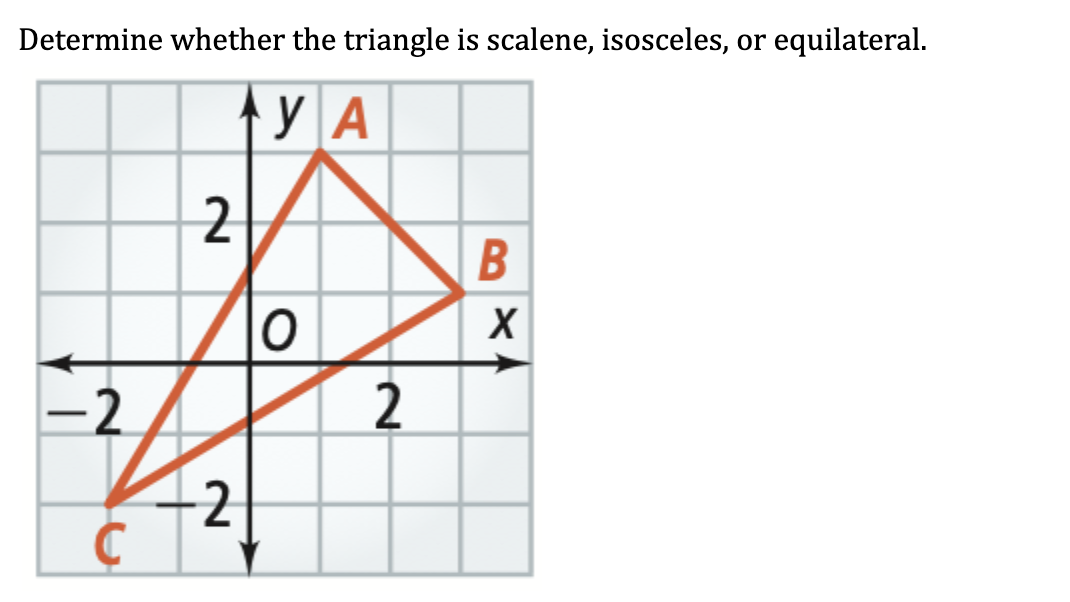
Determine whether the triangle is scalene, isosceles, or equilateral.
Understand the Problem
The question is asking us to determine the type of triangle formed by points A, B, and C. We will identify whether the triangle is scalene, isosceles, or equilateral by calculating the lengths of the sides based on the coordinates provided in the image.
Answer
The triangle is scalene.
Answer for screen readers
The triangle formed by points A, B, and C is scalene.
Steps to Solve
- Identify the Coordinates of Points A, B, and C
From the graph:
- Point A = (2, 2)
- Point B = (0, 2)
- Point C = (0, -2)
- Calculate the Lengths of the Sides
Using the distance formula:
$$ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} $$
-
Length AB:
$$ AB = \sqrt{(0 - 2)^2 + (2 - 2)^2} = \sqrt{(-2)^2 + 0^2} = \sqrt{4} = 2 $$ -
Length BC:
$$ BC = \sqrt{(0 - 0)^2 + (-2 - 2)^2} = \sqrt{0^2 + (-4)^2} = \sqrt{16} = 4 $$ -
Length AC:
$$ AC = \sqrt{(0 - 2)^2 + (-2 - 2)^2} = \sqrt{(-2)^2 + (-4)^2} = \sqrt{4 + 16} = \sqrt{20} = 2\sqrt{5} $$
- Classify the Triangle by Side Lengths
To determine the type of triangle:
- Scalene: All sides different
- Isosceles: Two sides equal
- Equilateral: All sides equal
In this case:
- (AB = 2)
- (BC = 4)
- (AC = 2\sqrt{5} \approx 4.47)
Since all three lengths are different, the triangle is scalene.
The triangle formed by points A, B, and C is scalene.
More Information
A scalene triangle is one where all sides are of different lengths. This type of triangle does not have any equal angles either, distinguishing it from isosceles and equilateral triangles.
Tips
- Confusing lengths: Double-check calculations of each side length to ensure accuracy.
- Misclassifying the triangle: Ensure that all three sides are compared correctly to classify the triangle type.
AI-generated content may contain errors. Please verify critical information