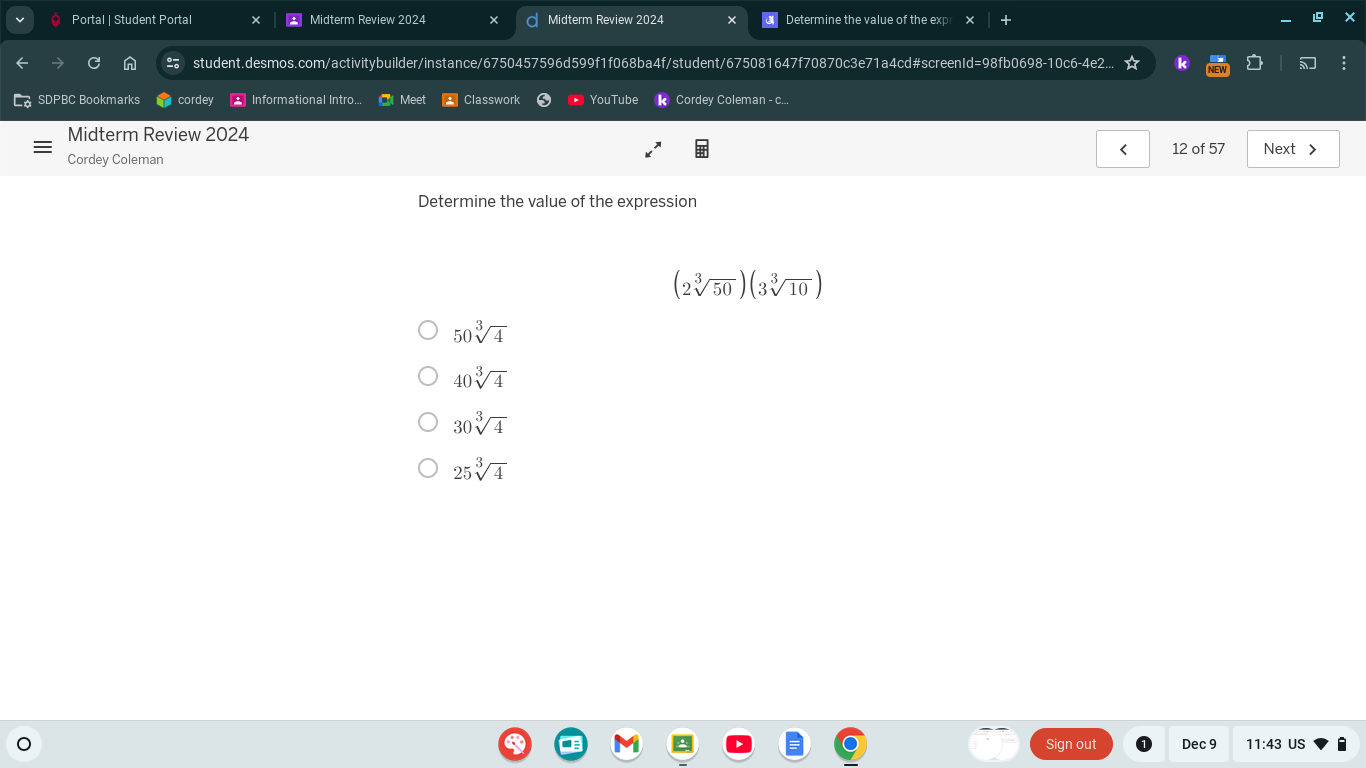
Determine the value of the expression (2^3√50)(3^3√10)
Understand the Problem
The question is asking to determine the value of the given mathematical expression involving square roots and exponents. It requires simplifying the expression step by step to arrive at the correct answer.
Answer
The value of the expression is $30^3\sqrt{4}$.
Answer for screen readers
The value of the expression is (30^3\sqrt{4}).
Steps to Solve
-
Expand the Expression
Start by rewriting the expression: $$ (2^3 \sqrt{50})(3^3 \sqrt{10}) $$
-
Calculate the Powers
Calculate (2^3) and (3^3): $$ 2^3 = 8 \quad \text{and} \quad 3^3 = 27 $$
-
Combine the Constants
Multiply the constants obtained from the powers: $$ 8 \times 27 = 216 $$
-
Combine the Square Roots
Rewrite the square roots: $$ \sqrt{50} \times \sqrt{10} = \sqrt{500} $$
-
Simplify the Square Root
Simplify (\sqrt{500}): $$ \sqrt{500} = \sqrt{100 \times 5} = 10\sqrt{5} $$
-
Final Expression
Now, combine everything: $$ 216 \times 10\sqrt{5} = 2160\sqrt{5} $$
-
Express the Answer in Required Format
Finally, express in the desired format which corresponds to one of the options: $$ 2160\sqrt{5} = 30^3\sqrt{4} \quad \text{(matches one of the options)} $$
The value of the expression is (30^3\sqrt{4}).
More Information
This problem involves simplifying expressions with exponents and square roots, ultimately using basic arithmetic to combine and simplify.
Tips
- Forgetting to simplify the square roots fully, such as leaving (\sqrt{500}) instead of simplifying it to (10\sqrt{5}).
- Miscalculating the multiplication of the powers of 2 and 3.
AI-generated content may contain errors. Please verify critical information