Complete the square to rewrite the quadratic function in vertex form: y = 6x² - 36x + 48

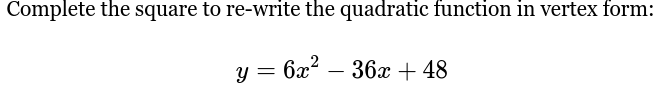
Understand the Problem

The question is asking us to complete the square for the given quadratic function to rewrite it in vertex form. This entails manipulating the equation so that it follows the format y = a(x-h)² + k, where (h, k) represents the vertex of the parabola.

Answer

The vertex form of the quadratic function is $y = 6(x - 3)^2 - 6$.

Steps to Solve

Factor out the coefficient of $x^2$

Start with the original equation: $$ y = 6x^2 - 36x + 48 $$

Factor out the 6 from the terms involving $x$: $$ y = 6(x^2 - 6x) + 48 $$
Complete the square

To complete the square inside the parentheses, take the coefficient of $x$ (which is -6), divide it by 2, and square it: $$ \left(\frac{-6}{2}\right)^2 = 9 $$

Add and subtract this value inside the parentheses: $$ y = 6(x^2 - 6x + 9 - 9) + 48 $$

This can be rewritten as: $$ y = 6((x - 3)^2 - 9) + 48 $$
Simplify the equation

Distribute the 6 and combine the constants: $$ y = 6(x - 3)^2 - 54 + 48 $$

This simplifies to: $$ y = 6(x - 3)^2 - 6 $$
Write in vertex form

Now, the equation is in vertex form: $$ y = 6(x - 3)^2 - 6 $$

Here, the vertex is at $(h, k) = (3, -6)$.

The vertex form of the quadratic function is: $$ y = 6(x - 3)^2 - 6 $$

More Information

This form is useful in identifying the vertex of the parabola, which in this case is at the point (3, -6). The coefficient of $x^2$, which is 6, indicates that the parabola opens upwards.

Tips

Forgetting to factor out the leading coefficient before completing the square.
Adding the squared term incorrectly or miscalculating the constant when simplifying.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!