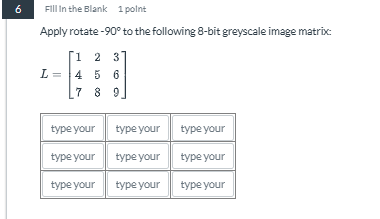
Apply rotate -90 to the following 8-bit greyscale image matrix: L = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]

Steps to Solve

1. Understanding the Rotation To rotate a matrix by -90 degrees, the first row becomes the last column, the second row becomes the second-last column, and so on.

2. Matrix Representation The original matrix is: $$ L = \begin{bmatrix} 1 & 2 & 3 \ 4 & 5 & 6 \ 7 & 8 & 9 \end{bmatrix} $$

3. Determine the New Indices For a -90-degree rotation, the new position of an element located at position $(i, j)$ in the original matrix will move to position $(j, n-1-i)$ in the new matrix, where $n$ is the number of rows (or columns since it's a square matrix).

4. Applying the New Positions For the given matrix, $n = 3$. Thus, for each element:

• $(0, 0) \rightarrow (0, 2)$
• $(0, 1) \rightarrow (1, 2)$
• $(0, 2) \rightarrow (2, 2)$
• $(1, 0) \rightarrow (0, 1)$
• $(1, 1) \rightarrow (1, 1)$
• $(1, 2) \rightarrow (2, 1)$
• $(2, 0) \rightarrow (0, 0)$
• $(2, 1) \rightarrow (1, 0)$
• $(2, 2) \rightarrow (2, 0)$

5. Constructing the Rotated Matrix Using the new indices:

• Position $(0, 2)$ is 1
• Position $(1, 2)$ is 4
• Position $(2, 2)$ is 7
• Position $(0, 1)$ is 2
• Position $(1, 1)$ is 5
• Position $(2, 1)$ is 8
• Position $(0, 0)$ is 3
• Position $(1, 0)$ is 6
• Position $(2, 0)$ is 9

This gives the new matrix: $$ L_{rotated} = \begin{bmatrix} 3 & 6 & 9 \ 2 & 5 & 8 \ 1 & 4 & 7 \end{bmatrix} $$